Cette distribution est une distribution réduite, comme la variable Z abordée au module 70. Elle est utilisée dans le cas où la variance σ2 de la population est inconnue.
La variance de la population (σ2) étant inconnue, elle doit être substituée par la seule variance à notre disposition: la variance de l'échantillon (S2). La réduction de Student est communément employée pour convertir une moyenne expérimentale en une valeur réduite selon l'application du Théorème de la limite centrale (voir ces quelques pages...).
La réduction d'une variable observée, ici la moyenne d'un échantillon, en une variable réduite t s'effectue comme suit:
Au lieu de :
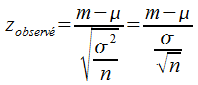
on remplace σ2 par S2 et on obtient :
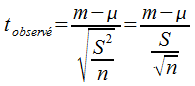
avec m la moyenne de l'échantillon, µ la moyenne de la population, S2 la variance de l'échantillon, et S l'écart-type de l'échantillon.
Cette valeur de t observée tient compte de la taille de l'échantillon, car plus n est grand, plus S estime correctement σ. La précision de cette estimation est prise en compte dans le modèle mathématique de la distribution de Student à travers le degré de liberté (k=n-1), qui augmente d'autant plus que n augmente.
Comme la variable réduite Z (voir module 70) la variable réduite t a pour moyenne 0, mais sa variance n'est plus 1, elle est toujours > 1, mais d'autant plus proche de 1 que son degré de liberté est grand. Lorsque n = ∞, t v.a. N(0;1). Donc lorsque n = ∞ -> t=z.
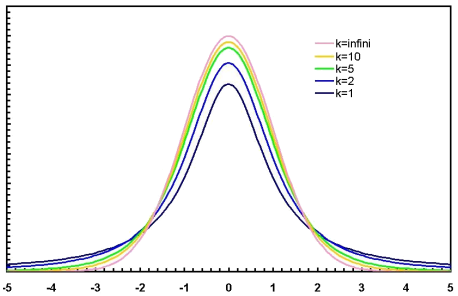
D'après Thorin sur fr.wikipedia.org
La variance de la distribution de Student dépendant de son degré de liberté, la table de Student corrige les valeurs réduites pour les différentes probabilités en tenant compte du degré de liberté utilisé (k) .
Exemple : Cherchons dans les tables la valeur réduite en dessous de laquelle on trouve 95% des individus :
Dans le cas de z v.a. N(0;1) si P(Z<z)=0,95 -> z=1,645
Dans le cas d'une distribution de Student avec k=40 degrés de liberté : t40;0,95 = 1,684
Dans le cas d'une distribution de Student avec k=20 degrés de liberté : t20;0,95 = 1,725
Dans le cas d'une distribution de Student avec k=10 degrés de liberté : t10;0,95 = 1,812
Dans le cas d'une distribution de Student avec k=5 degrés de liberté : t5;0,95 = 2,015
...

