Le théorème central limite est un théorème mathématique qui explique les paramètres de la distribution d'échantillonnage, ou distribution des moyennes des échantillons.
Selon le théorème central limite, les moyennes des échantillons indépendants provenant d'une même population (µ;σ²) se distribuent elles aussi selon une distribution normale de paramètres (µ;σ²/n).
Illustration avec une variable normale
Soient x1, x2, x3 ... x∞ les tailles (cm) de truites arc-en-ciel. La taille de ces truites se distribue selon une distribution normale de paramètres :
X v.a. N(µ;σ²)
Si on réalise des échantillons indépendants (les poissons sont choisis au hasard) de n individus, toutes les moyennes de ces échantillons se distribuent selon une distribution normale de même moyenne, mais de variance plus faible, avec σ²moyennes = σ²individus / n.
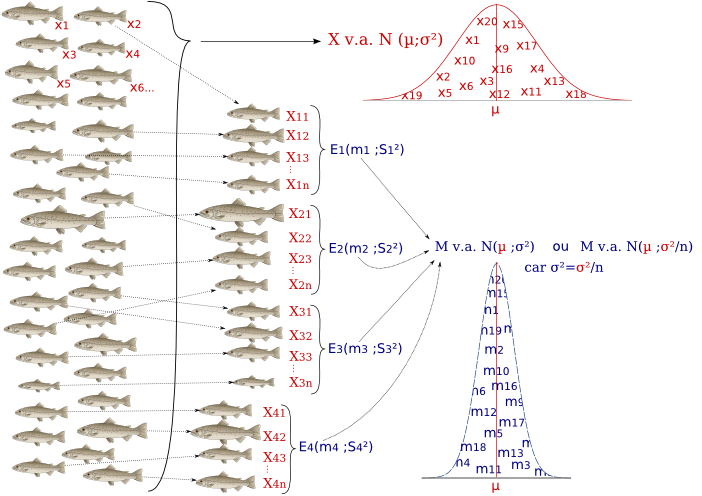
Exemples :
Si les truites proviennent d'une population de paramètres (15;4), les échantillons de 4 truites auront des moyennes qui se distribuent selon un modèle Normal de paramètres (15;1).
Si les truites proviennent d'une population de paramètres (20;12), les échantillons de 3 truites auront des moyennes qui se distribuent selon un modèle Normal de paramètres (20;4).
etc...
Illustration avec une variable Binomiale
Le théorème central limite s'applique aussi aux distributions discontinues telles que les distributions Binomiales ou de Poisson.
Prenons le cas du lancer d'un dé. Si le dé a 6 faces, et qu'il est équilibré, chaque face a 1/6ème de chance d'être affichée lors d'un lancer.
Si je lance le dé une seule fois, P(face=1)=P(face=3)=1/6
Si je lance le dé 10 fois P(moyenne=1)<P(moyenne=3)
Si je lance le dé 100 fois P(moyenne=1)<<<<<<P(moyenne=3)
etc...
Même si la variable est discontinue, la distribution des valeurs des moyennes des échantillons sera normale de paramètres (µ;σ²/n) avec µ=moyenne de la population des valeurs de départ, et σ² la variance de cette population de départ.
Conséquence du théorème central limite
Lorsqu'on dispose des données de population (µ;σ²) et qu'on vous demande de calculer des probabilités associées à des valeurs moyennes réalisées sur n mesures, vous devez replacer ces valeurs moyennes dans leur distribution (µ;σ²/n) et non pas dans la distribution des valeurs des individus (µ;σ²).

