Module 70:

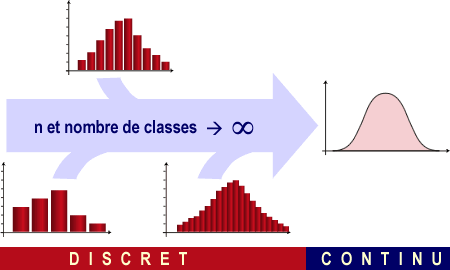
Dans une population de chauves-souris, la totalité des individus peut être rangée dans des classes d'intervalles constants comme décrit précédemment dans les statistiques descriptives à une dimension.

La population est composée d'un grand nombre d'individus que l'on peut classer dans une infinité de classes d'intervalles Li tendant vers 0. L'histogramme est alors remplacé par une courbe de Gauss-Laplace:

Pour des échantillons de taille finie, l'ordonnée de l'histogramme se représente par des densités de fréquences relatives alors que pour la population on parle de densités de probabilités. (n tend vers l'infini et delta x tend vers 0)

1. équation et symbolique
2. symétrie autour de la moyenne
3. modification de la variance

Equation et symbolique

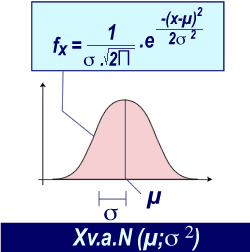
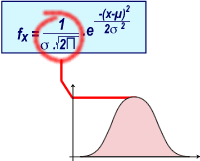
La distribution normale se caractérise par une équation faisant intervenir la moyenne µ et la variance σ². Par convention, nous adopterons la convention d'écriture: X v.a.N(µ; σ²) . Dans la littérature, on peut aussi trouver: µ± σ ( moyenne ± écart-type).

Symétrie autour de la moyenne

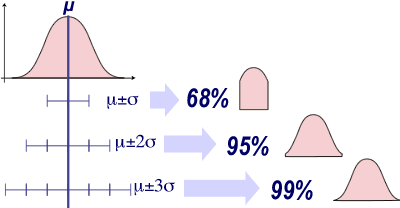
La courbe de Gauss-Laplace est symétrique:

1. Lorsqu'on sélectionne l'intervalle compris entre +1 et -1 écart-type autour de la moyenne µ (de μ-σ jusque μ+σ), on isole 68% des individus d'une population normale.
2. Lorsqu'on sélectionne l'intervalle compris entre +2 et -2 écarts-types autour de la moyenne µ (de μ-2σ jusque μ+2σ), on isole 95% des individus d'une population normale.
3. Lorsqu'on sélectionne l'intervalle compris entre +3 et -3 écarts-types autour de la moyenne µ (de μ-3σ jusque μ+3σ), on isole 99% des individus d'une population normale.

Modification de la variance

Lorsque la variance d'une population diminue, cela se traduit par une dispersion moins importante de la courbe autour de la moyenne. Concomitamment, le sommet de la courbe tend à s'élever afin de préserver une surface totale sous la courbe égale à 1 (ou 100%).

Dans une population de chauves-souris de l'espèce A, l'envergure X est une v.a. N(375; 225)
Dans une population de chauves-souris de l'espèce A femelles, l'envergure X est une v.a. N(375; 121)
Dans une population de chauves-souris de l'espèce A femelles de 3 mois, l'envergure X est une v.a. N(375; 49)
etc.

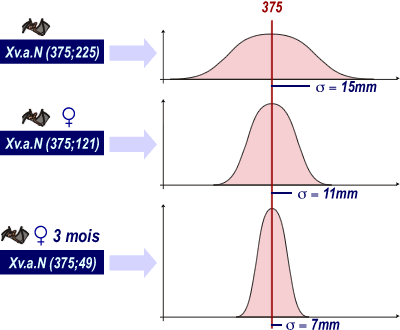
Influence de la variance sur le sommet de la courbe de Gauss: Si la variance diminue, le sommet de la courbe tend à augmenter. En effet, dans l'équation de la courbe, l'écart-type se trouve au dénominateur(voir terme entouré en rouge). Plus l'écart-type est petit, plus ce terme tend à devenir grand...

Chaque v.a. Normale possède sa propre moyenne (µ) et variance (²). Déterminer des probabilités sous ce type de courbes de Gauss (à chaque cas particulier est associée une courbe de moyenne et de variance particulière) requiert un algorithme d'intégration numérique.

Heureusement, toutes les v.a. Normales peuvent se réduire à une seule et même distribution normale Z. La distribution réduite de Z est centrée sur une moyenne 0 et possède une variance 1. La table de probabilité de Z a été calculée une fois pour toutes et dispense des probabilités du type:

P(Zzi)

Comment réduire?

Toutes les distributions normales (v.a.N) peuvent être ramenées à une distribution obéissant aussi à la loi normale. Cette distribution est obtenue par la réduction de la variable étudiée X en une variable réduite appelée Z.

Cette distribution est centrée sur la moyenne 0 et possède une variance 1 et est symbolisée de la façon suivante:

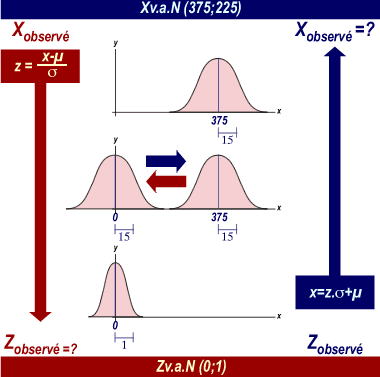
Xobservé = 390 et X v.a.N (375;225)

alors Zobservé = (390-375)/(racine carrée de 225) = 15/15 = 1

Zobservé = 2,5 et X v.a.N (375;225)

alors Xobservé = 2,5.(racine carrée de 225) + 375=412,5

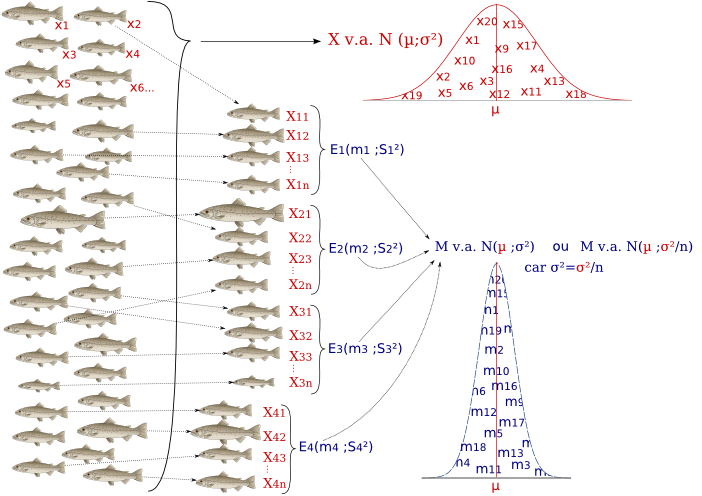
Le théorème central limite est un théorème mathématique qui explique les paramètres de la distribution d'échantillonnage, ou distribution des moyennes des échantillons.

Selon le théorème central limite, les moyennes des échantillons indépendants provenant d'une même population (µ;σ²) se distribuent elles aussi selon une distribution normale de paramètres (µ;σ²/n).

Illustration avec une variable normale

Soient x₁, x₂, x₃ ... x_∞ les tailles (cm) de truites arc-en-ciel. La taille de ces truites se distribue selon une distribution normale de paramètres :

X v.a. N(µ;σ²)

Si on réalise des échantillons indépendants (les poissons sont choisis au hasard) de n individus, toutes les moyennes de ces échantillons se distribuent selon une distribution normale de même moyenne, mais de variance plus faible, avec σ²_moyennes = σ²_individus / n.

Exemples :

Si les truites proviennent d'une population de paramètres (15;4), les échantillons de 4 truites auront des moyennes qui se distribuent selon un modèle Normal de paramètres (15;1).

Si les truites proviennent d'une population de paramètres (20;12), les échantillons de 3 truites auront des moyennes qui se distribuent selon un modèle Normal de paramètres (20;4).

etc...

Illustration avec une variable Binomiale

Le théorème central limite s'applique aussi aux distributions discontinues telles que les distributions Binomiales ou de Poisson.

Prenons le cas du lancer d'un dé. Si le dé a 6 faces, et qu'il est équilibré, chaque face a 1/6ème de chance d'être affichée lors d'un lancer.

Si je lance le dé une seule fois, P(face=1)=P(face=3)=1/6

Si je lance le dé 10 fois P(moyenne=1)<P(moyenne=3)

Si je lance le dé 100 fois P(moyenne=1)<<<<<<P(moyenne=3)

etc...

Même si la variable est discontinue, la distribution des valeurs des moyennes des échantillons sera normale de paramètres (µ;σ²/n) avec µ=moyenne de la population des valeurs de départ, et σ² la variance de cette population de départ.

Conséquence du théorème central limite

Lorsqu'on dispose des données de population (µ;σ²) et qu'on vous demande de calculer des probabilités associées à des valeurs moyennes réalisées sur n mesures, vous devez replacer ces valeurs moyennes dans leur distribution (µ;σ²/n) et non pas dans la distribution des valeurs des individus (µ;σ²).

Utilisation de la table de Z:

La table de Z (accessible depuis le lien "Tables" en haut de toutes les pages de ce site) vous donne les probabilités associées à des valeurs de z selon la relation p(Z<z).

Exemple : quelle est la probabilité d'être inférieur à un z de 1,96 dans une distribution de z v.a. N(0;1) ?
La table vous donne la réponse :
En tête de ligne on trouve la valeur entière et la première décimale de la valeur z.
En tête de colonne on trouve la seconde décimale de z.

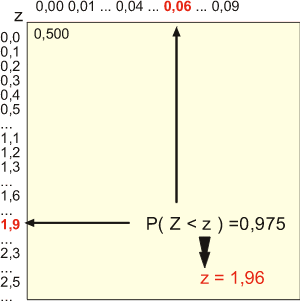
Donc P(Z<1,96)=0,975=97,5%

Inconvénient de la table de Z :

On peut la lire à l'envers donc par déduction on peut y trouver les valeurs de Z qui correspondent à une certaine probabilité.
Cependant toutes les probabilités intéressantes ne sont pas forcément représentées.
Si par exemple on cherche le z en dessous duquel il y a 98,5% des individus, on cherche la valeur 0,985 dans les valeurs du tableau, et en regardant les en-têtes de ligne et de colonne je trouve que le z qui correspond est 2,17 (ligne 2,1 et colonne 0,07).
Mais si je cherche le z tel que P(Z<z)=0,8=80%, il n'y a pas 0,8 dans les valeurs. On passe de 0,79955 à 0,80234, donc le z tel que P(Z<z)=0,8 est compris entre 0,84 et 0,85.

Cette table peut donc s'employer dans le sens :
z connu --> trouver la probabilité P(Z ≤ z)
ou dans le sens :
probabilité P(Z ≤ z) connue--> trouver le z correspondant, mais elle n'est pas pratique dans ce sens là.

Utilisation de la table de Student :

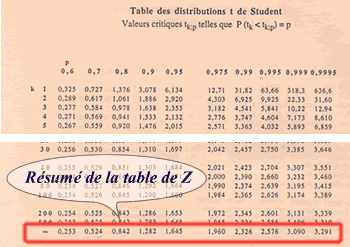
La table de Student part des probabilités et donne les valeurs des variables réduites correspondantes (z ou t).
Si la variance de la population est connue (σ²), on peut employer la table de t de Student comme s'il s'agissait d'une table simplifiée de Z.
L'avantage d'une telle table est de pouvoir donner rapidement des valeurs de Z ou des probabilités très couramment utilisées dans les tests d'hypothèses (voir l'emploi des intervalles de confiance).

• En tête de colonne (p): donne la probabilité P(Z ≤ z)
• En tête de ligne (k): se positionner en l'"infini"

Dans notre exemple précédent :

P(Z<z)=0,8=80% donne ici directement une valeur exacte de 0,842.

En conclusion :

Pour trouver une probabilité à partir d'une valeur de z : on utilise la table de Z.

Pour trouver une valeur de z à partir d'une probabilité : on utilise la table de student, dernière ligne.

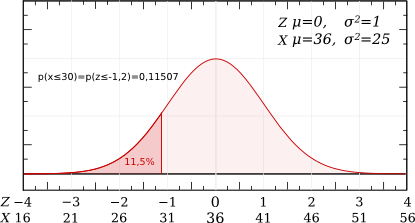
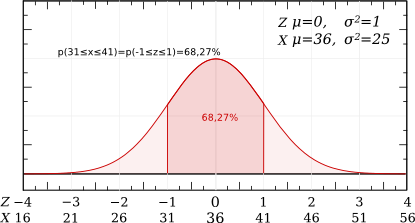
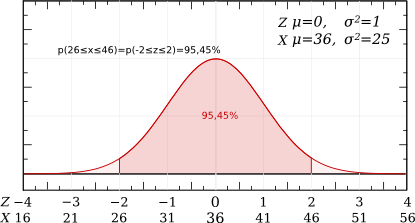
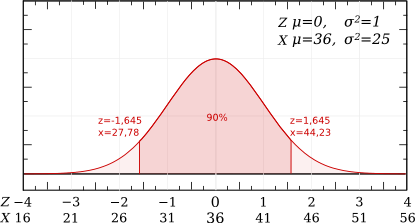
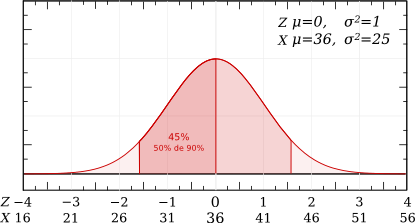
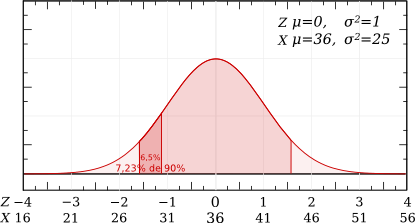
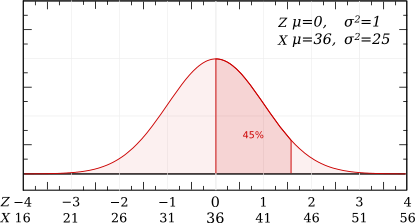
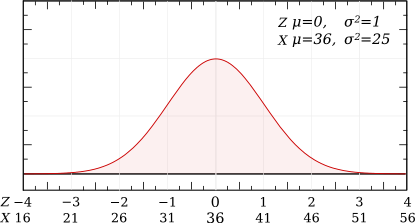
Une vache produit quotidiennement 36 ± 5 litres de lait.

1. Définissez la variable étudiée et ses paramètres. Correction.
2. Quelle est la probabilité qu'une vache prise au hasard ait une production laitière inférieure à 30 L/jour ? Correction.
3. Quelle est la probabilité que la production laitière soit comprise entre :
   1. la moyenne plus ou moins 1 écart -type ? Correction.
   2. la moyenne plus ou moins 2 écarts -types ? Correction.
4. La population comprend 5 % de vaches considérées comme étant des mauvaises productrices (faible production laitière), et 5 % de vaches considérées comme étant des excellentes productrices (production laitière élevée). Le reste de la population est considéré comme peuplé de vaches à production correcte. A partir de quelle production journalière peut-on considérer qu'une vache est mauvaise productrice ou excellente productrice ? Correction.
5. Quelle est la probabilité qu'une productrice correcte produise moins de 36 L/jour ? Correction.
6. Quelle est la probabilité qu'une productrice correcte ait une production inférieure à 30 L/jour ? Correction.
7. Quelle est la probabilité qu'une vache ayant une production inférieure à 30 L/jour soit une productrice correcte ? Correction.
8. Quelle est la probabilité qu'une vache prise au hasard soit une productrice laitière correcte et ai une production supérieure à 36 L/jour ? Correction.

Pour répondre vous devez consulter les tables.

Enoncé :

Une vache produit quotidiennement 36 ± 5 litres de lait.

Questions :

1. Définissez la variable étudiée et ses paramètres.

Correction :
Variable étudiée : la production quotidienne de lait chez la vache, mesurée en litres.
Paramètres : Moyenne : 36 l; Ecart-type : 5 l.
Retour à l'énoncé.




2. Quelle est la probabilité qu'une vache prise au hasard ait une production laitière inférieure à 30 L/jour ?

Correction :
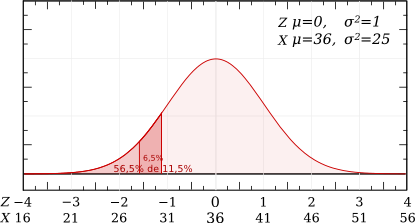
Z=(30-36)/5=-6/5=-1,2.
La probabilité d'être inférieur à -1,2 correspond à celle d'être supérieur à 1,2 : p(Z≤-1,2)=p(Z≥1,2)
La probabilité d'être supérieur à 1,2 = 1 - Probabilité d'être inférieur à 1,2 : p(Z ≥ 1,2) = 1-p(Z≤1,2)
Dans les tables on trouve : Probabilité d'être inférieur à 1,2 = 0,88493.
Donc p(Z≤-1,2) = 1 - 0,88493 = 0,11507, c'est à dire 11,5%.
Retour à l'énoncé.




3. Quelle est la probabilité que la production laitière soit comprise entre :
   
   1. la moyenne plus ou moins 1 écart -type ?
      
      Correction :
      p(-1≤Z≤1) = p(Z≤1) - p(Z≤-1) = p(Z≤1) - (1-p(Z≤1)) = 0,84135 - (1 - 0,84135) = 0,68270, soit approximativement 68%.
      Retour à l'énoncé.
      
      
      
      
   2. la moyenne plus ou moins 2 écarts -types ?
      
      Correction :
      p(-2≤Z≤2) = p(Z≤2) - p(Z≤-2) = p(Z≤2) - (1-p(Z≤2)) = 0,97725 - (1 - 0,97725) = 0,95450, soit approximativement 95%.
      Retour à l'énoncé.
      
      
      
      
4. La population comprend 5 % de vaches considérées comme étant des mauvaises productrices (faible production laitière), et 5 % de vaches considérées comme étant des excellentes productrices (production laitière élevée). Le reste de la population est considéré comme peuplé de vaches à production correcte. A partir de quelle production journalière peut-on considérer qu'une vache est mauvaise productrice ou excellente productrice ?
   
   Correction :
   Recherche des z correspondants à ces probabilités :
   p(Z≤z₁)=0,95 -> Table de Student, dernière ligne (∞) pour une confiance de 95% : z₁ = 1,645.
   Alors p(Z≤z₂)=0,05 -> z₂ = -1,645.
   Calcul des x correspondants aux z :
   Sachant que z=(x-µ)/σ alors x=(z. σ)+µ
   Pour z₁ = 1,645 : x₁= (1,645x5) + 36 = 44,23
   Pour z₂ = -1,645 : x₂= (-1,645x5) + 36 = 27,78
   Retour à l'énoncé.
   
   
   
   
5. Quelle est la probabilité qu'une productrice correcte produise moins de 36 L/jour ?
   
   Correction :
   p(X≤36) dans la population globale = 0,5 ou 50%, car 36 est la moyenne de la population.
   Ici la répartition du critère "production correcte de lait" est symétrique à la moyenne, donc "p(X≤36) sachant que les vaches sont correctes" est aussi de 50%.
   Démonstration pour les sceptiques :
   La population des productrices correctes ne comprend pas toutes les vaches, seulement celles dont la production est comprise entre 27,78 et 44,23 l/j, c'est à dire 90% de la population. Pour résoudre cet exercice on va calculer :
   p(X≤36) sachant que x appartient à "production correcte ".
   Petit rappel de probabilités : P(A/B) = P(A∩B)/p(B)
   Donc : p(X≤36) parmi les vaches à production correcte = p(27,78≤X≤36)/p(27,78≤X≤44,23)=0,45/0,9=0,5.
   Retour à l'énoncé.
   
   
   
   
6. Quelle est la probabilité qu'une productrice correcte ait une production inférieure à 30 L/jour ??
   
   Correction :
   Même principe :
   p(X≤30) parmi les vaches normales = p(27,78≤X≤30)/p(27,78≤X≤44,23)
   p(27,78≤X≤30)=0,11507-0,05=0,06507
   Donc : probabilité qu'une productrice normale ait une production inférieure à 30 l/jour = 0,06507/0,9=0,0723 c'est à dire 7,23%
   Retour à l'énoncé.
   
   
   
   
7. Quelle est la probabilité qu'une vache ayant une production inférieure à 30 L/jour soit une productrice correcte ?
   
   Correction :
   Revient à faire :
   p(27,78≤X≤30)/p(X≤30)=0,06507/0,11507=0,56548... c'est à dire 56,5%
   Retour à l'énoncé.
   
   
   
   
8. Quelle est la probabilité qu'une vache prise au hasard soit une productrice laitière correcte et ai une production supérieure à 36 L/jour ?
   
   Correction :
   p(36≤X≤44,23)= p(X≤44,23) - p(X≤36)=0,95-0,50=0,45 c'est à dire 45%.
   Retour à l'énoncé.