Enoncé :

Une vache produit quotidiennement 36 ± 5 litres de lait.

Questions :

1. Définissez la variable étudiée et ses paramètres.

Correction :
Variable étudiée : la production quotidienne de lait chez la vache, mesurée en litres.
Paramètres : Moyenne : 36 l; Ecart-type : 5 l.
Retour à l'énoncé.




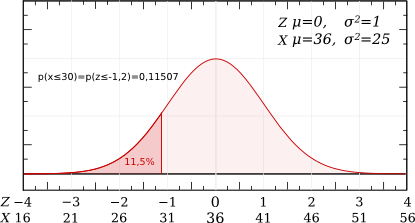
2. Quelle est la probabilité qu'une vache prise au hasard ait une production laitière inférieure à 30 L/jour ?

Correction :
Z=(30-36)/5=-6/5=-1,2.
La probabilité d'être inférieur à -1,2 correspond à celle d'être supérieur à 1,2 : p(Z≤-1,2)=p(Z≥1,2)
La probabilité d'être supérieur à 1,2 = 1 - Probabilité d'être inférieur à 1,2 : p(Z ≥ 1,2) = 1-p(Z≤1,2)
Dans les tables on trouve : Probabilité d'être inférieur à 1,2 = 0,88493.
Donc p(Z≤-1,2) = 1 - 0,88493 = 0,11507, c'est à dire 11,5%.
Retour à l'énoncé.




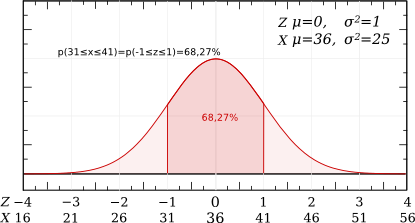
3. Quelle est la probabilité que la production laitière soit comprise entre :
   
   1. la moyenne plus ou moins 1 écart -type ?
      
      Correction :
      p(-1≤Z≤1) = p(Z≤1) - p(Z≤-1) = p(Z≤1) - (1-p(Z≤1)) = 0,84135 - (1 - 0,84135) = 0,68270, soit approximativement 68%.
      Retour à l'énoncé.
      
      
      
      
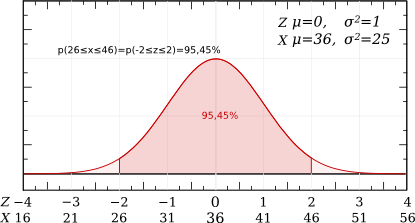
   2. la moyenne plus ou moins 2 écarts -types ?
      
      Correction :
      p(-2≤Z≤2) = p(Z≤2) - p(Z≤-2) = p(Z≤2) - (1-p(Z≤2)) = 0,97725 - (1 - 0,97725) = 0,95450, soit approximativement 95%.
      Retour à l'énoncé.
      
      
      
      
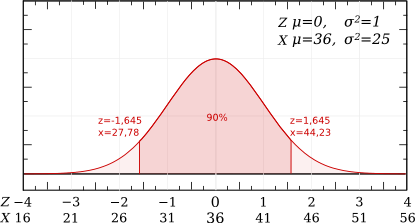
4. La population comprend 5 % de vaches considérées comme étant des mauvaises productrices (faible production laitière), et 5 % de vaches considérées comme étant des excellentes productrices (production laitière élevée). Le reste de la population est considéré comme peuplé de vaches à production correcte. A partir de quelle production journalière peut-on considérer qu'une vache est mauvaise productrice ou excellente productrice ?
   
   Correction :
   Recherche des z correspondants à ces probabilités :
   p(Z≤z₁)=0,95 -> Table de Student, dernière ligne (∞) pour une confiance de 95% : z₁ = 1,645.
   Alors p(Z≤z₂)=0,05 -> z₂ = -1,645.
   Calcul des x correspondants aux z :
   Sachant que z=(x-µ)/σ alors x=(z. σ)+µ
   Pour z₁ = 1,645 : x₁= (1,645x5) + 36 = 44,23
   Pour z₂ = -1,645 : x₂= (-1,645x5) + 36 = 27,78
   Retour à l'énoncé.
   
   
   
   
5. Quelle est la probabilité qu'une productrice correcte produise moins de 36 L/jour ?
   
   Correction :
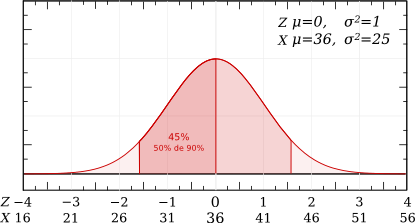
   p(X≤36) dans la population globale = 0,5 ou 50%, car 36 est la moyenne de la population.
   Ici la répartition du critère "production correcte de lait" est symétrique à la moyenne, donc "p(X≤36) sachant que les vaches sont correctes" est aussi de 50%.
   Démonstration pour les sceptiques :
   La population des productrices correctes ne comprend pas toutes les vaches, seulement celles dont la production est comprise entre 27,78 et 44,23 l/j, c'est à dire 90% de la population. Pour résoudre cet exercice on va calculer :
   p(X≤36) sachant que x appartient à "production correcte ".
   Petit rappel de probabilités : P(A/B) = P(A∩B)/p(B)
   Donc : p(X≤36) parmi les vaches à production correcte = p(27,78≤X≤36)/p(27,78≤X≤44,23)=0,45/0,9=0,5.
   Retour à l'énoncé.
   
   
   
   
6. Quelle est la probabilité qu'une productrice correcte ait une production inférieure à 30 L/jour ??
   
   Correction :
   Même principe :
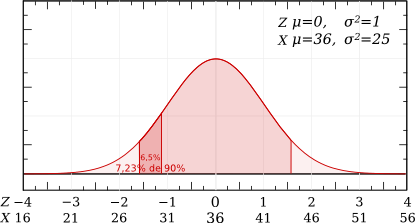
   p(X≤30) parmi les vaches normales = p(27,78≤X≤30)/p(27,78≤X≤44,23)
   p(27,78≤X≤30)=0,11507-0,05=0,06507
   Donc : probabilité qu'une productrice normale ait une production inférieure à 30 l/jour = 0,06507/0,9=0,0723 c'est à dire 7,23%
   Retour à l'énoncé.
   
   
   
   
7. Quelle est la probabilité qu'une vache ayant une production inférieure à 30 L/jour soit une productrice correcte ?
   
   Correction :
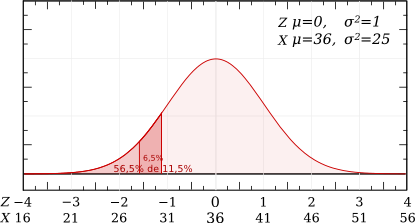
   Revient à faire :
   p(27,78≤X≤30)/p(X≤30)=0,06507/0,11507=0,56548... c'est à dire 56,5%
   Retour à l'énoncé.
   
   
   
   
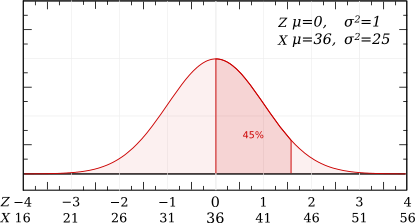
8. Quelle est la probabilité qu'une vache prise au hasard soit une productrice laitière correcte et ai une production supérieure à 36 L/jour ?
   
   Correction :
   p(36≤X≤44,23)= p(X≤44,23) - p(X≤36)=0,95-0,50=0,45 c'est à dire 45%.
   Retour à l'énoncé.