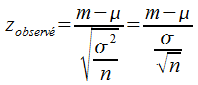
Les contenus sont © P. Calmant et E. Depiereux - 2004; G. Vincke B. De Hertogh et E. Depiereux 2008.
Imprimé le
12/3/2026
Cette distribution est une distribution réduite, comme la variable Z abordée au module 70. Elle est utilisée dans le cas où la variance σ2 de la population est inconnue.
La variance de la population (σ2) étant inconnue, elle doit être substituée par la seule variance à notre disposition: la variance de l'échantillon (S2). La réduction de Student est communément employée pour convertir une moyenne expérimentale en une valeur réduite selon l'application du Théorème de la limite centrale (voir ces quelques pages...).
La réduction d'une variable observée, ici la moyenne d'un échantillon, en une variable réduite t s'effectue comme suit:
Au lieu de :
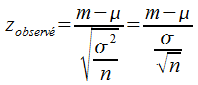
on remplace σ2 par S2 et on obtient :
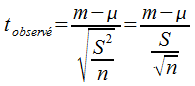
avec m la moyenne de l'échantillon, µ la moyenne de la population, S2 la variance de l'échantillon, et S l'écart-type de l'échantillon.
Cette valeur de t observée tient compte de la taille de l'échantillon, car plus n est grand, plus S estime correctement σ. La précision de cette estimation est prise en compte dans le modèle mathématique de la distribution de Student à travers le degré de liberté (k=n-1), qui augmente d'autant plus que n augmente.
Comme la variable réduite Z (voir module 70) la variable réduite t a pour moyenne 0, mais sa variance n'est plus 1, elle est toujours > 1, mais d'autant plus proche de 1 que son degré de liberté est grand. Lorsque n = ∞, t v.a. N(0;1). Donc lorsque n = ∞ -> t=z.
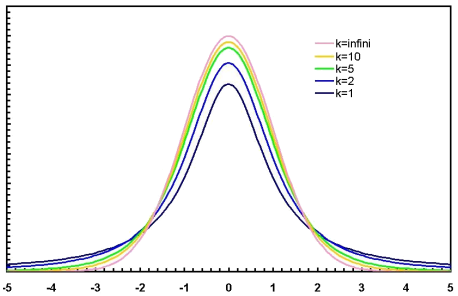
D'après Thorin sur fr.wikipedia.org
La variance de la distribution de Student dépendant de son degré de liberté, la table de Student corrige les valeurs réduites pour les différentes probabilités en tenant compte du degré de liberté utilisé (k) .
Exemple : Cherchons dans les tables la valeur réduite en dessous de laquelle on trouve 95% des individus :
Dans le cas de z v.a. N(0;1) si P(Z<z)=0,95 -> z=1,645
Dans le cas d'une distribution de Student avec k=40 degrés de liberté : t40;0,95 = 1,684
Dans le cas d'une distribution de Student avec k=20 degrés de liberté : t20;0,95 = 1,725
Dans le cas d'une distribution de Student avec k=10 degrés de liberté : t10;0,95 = 1,812
Dans le cas d'une distribution de Student avec k=5 degrés de liberté : t5;0,95 = 2,015
...
Exercice 1: Soit une population de chauves-souris dont on connait la longueur moyenne des oreilles (µ=23 mm). On prélève un échantillon de 21 chauves-souris dont la longueur moyenne des oreilles est de 22,34 mm avec une variance de 49 mm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ? Correction
Exercice 2: Soit une population de chauves-souris dont on connait la longueur moyenne des oreilles (µ=23 mm). On prélève un échantillon de 21 chauves-souris dont la longueur moyenne des oreilles est de 20,5 mm avec une variance de 16 mm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ? Correction
Exercice 3: Pour une population de vipères à collier adultes, on enregistre une longueur moyenne de corps de 130 cm. Sachant qu'on prélève un échantillon de 9 individus dont la longueur moyenne est de 133,33 cm avec une variance de 81 cm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ? Qu'en est-il avec un autre échantillon de 9 individus dont la moyenne vaut 139 cm et de même variance que le précédent ? Correction
Soit une population de chauves-souris dont on connait la longueur moyenne des oreilles (µ=23 mm). On prélève un échantillon de 21 chauves-souris dont la longueur moyenne des oreilles est de 22,34 mm avec une variance de 49 mm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ?
Correction :
On ne connait pas la variance de la population (σ2), donc on l'estime avec la valeur de la variance de l'échantillon : S2 = 49 mm2, ce qui donne un écart-type S = 7 mm.
Avec ces données on peut calculer un t observé = 22,34-23/(7/racine de 21) = -0,432.
Cette valeur de t est associée à un certain nombre de degrés de liberté : si l'échantillon est composé de 21 individus, le degré de liberté est de n-1=21-1=20.
L'intervalle comprenant les 95% des valeurs les plus fréquentes autour de la moyenne de la population va donc de t20;0,025 à t20;0,975.
La lecture de la table de Student nous donne les valeurs suivantes :
t20;0,975 = 2,086 (ligne 20, colonne 0,975).
La distribution de Student étant symétrique par rapport à sa moyenne on a :
t20;0,025 = -2,086
Notre valeur de t observé = -0,432. Elle est donc bien comprise dans cet intervalle, et on peut donc conclure que la moyenne de cet échantillon se situe effectivement dans les 95% des moyennes les plus plausibles autour de la moyenne de la population.
Retour aux énoncés
Soit une population de chauves-souris dont on connait la longueur moyenne des oreilles (µ=23 mm). On prélève un échantillon de 21 chauves-souris dont la longueur moyenne des oreilles est de 20,5 mm avec une variance de 16 mm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ?
Correction :
On ne connait pas la variance de la population (σ2), donc on l'estime avec la valeur de la variance de l'échantillon : S2 = 16 mm2, ce qui donne un écart-type S = 4 mm.
Avec ces données on peut calculer un t observé = 20,5-23/(4/racine de 21) = -2,864.
Cette valeur de t est associée à un certain nombre de degrés de liberté : si l'échantillon est composé de 21 individus, le degré de liberté est de n-1=21-1=20.
L'intervalle comprenant les 95% des valeurs les plus fréquentes autour de la moyenne de la population va donc de t20;0,025 à t20;0,975.
La lecture de la table de Student nous donne les valeurs suivantes :
t20;0,975 = 2,086 (ligne 20, colonne 0,975).
La distribution de Student étant symétrique par rapport à sa moyenne on a :
t20;0,025 = -2,086
Notre valeur de t observé = -2,864. Elle n'est donc pas comprise dans cet intervalle, et on peut donc conclure que la moyenne de cet échantillon ne se situe pas dans les 95% des moyennes les plus plausibles autour de la moyenne de la population.
Retour aux énoncés
Pour une population de vipères à collier adultes, on enregistre une longueur moyenne de corps de 130 cm. Sachant qu'on prélève un échantillon de 9 individus dont la longueur moyenne est de 133,33 cm avec une variance de 81 cm2. La moyenne de cet échantillon se situe-t-elle dans les 95% des moyennes les plus plausibles autour de la moyenne de la population ? Qu'en est-il avec un autre échantillon de 9 individus dont la moyenne vaut 139 cm et de même variance que le précédent ?
Correction :
Pour une moyenne m=133,33:
On ne connait pas la variance de la population (σ2), donc on l'estime avec la valeur de la variance de l'échantillon : S2 = 81 cm2, ce qui donne un écart-type S = 9 cm.
Avec ces données on peut calculer un t observé = 133,33-130/(9/3) = 1,11.
Cette valeur de t est associée à un certain nombre de degrés de liberté : si l'échantillon est composé de 9 individus, le degré de liberté est de n-1=9-1=8.
L'intervalle comprenant les 95% des valeurs les plus fréquentes autour de la moyenne de la population va donc de t8;0,025 à t8;0,975.
La lecture de la table de Student nous donne les valeurs suivantes :
t8;0,975 = 2,306 (ligne 8, colonne 0,975).
La distribution de Student étant symétrique par rapport à sa moyenne on a :
t8;0,025 = -2,306
Notre valeur de t observé = 1,11. Elle est donc bien comprise dans cet intervalle, et on peut donc conclure que la moyenne de cet échantillon se situe effectivement dans les 95% des moyennes les plus plausibles autour de la moyenne de la population.
Pour une moyenne m=139:
On ne connait pas la variance de la population (σ2), donc on l'estime avec la valeur de la variance de l'échantillon : S2 = 81 cm2, ce qui donne un écart-type S = 9 cm.
Avec ces données on peut calculer un t observé = 139-130/(9/3) = 3.
Cette valeur de t est associée à un certain nombre de degrés de liberté : si l'échantillon est composé de 9 individus, le degré de liberté est de n-1=9-1=8.
L'intervalle comprenant les 95% des valeurs les plus fréquentes autour de la moyenne de la population va donc de t8;0,025 à t8;0,975.
La lecture de la table de Student nous donne les valeurs suivantes :
t8;0,975 = 2,306 (ligne 8, colonne 0,975).
La distribution de Student étant symétrique par rapport à sa moyenne on a :
t8;0,025 = -2,306
Notre valeur de t observé = 3. Elle n'est donc pas comprise dans cet intervalle, et on peut donc conclure que la moyenne de cet échantillon ne se situe pas dans les 95% des moyennes les plus plausibles autour de la moyenne de la population. Retour aux énoncés