Test de comparaison de 2 moyennes provenant de 2 échantillons tirés de 2 populations indépendantes

 

Principe:

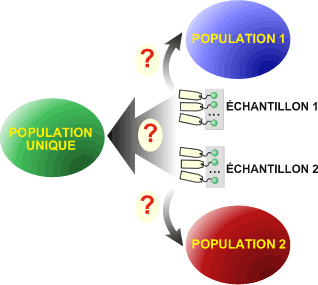
Un expérimentateur désire comparer les moyennes (m1 et m2) de deux échantillons composés d'individus distincts: les individus de l'échantillon 1 ne sont pas les mêmes que ceux de l'échantillon 2! Les deux échantillons sont indépendants.

La question est : les deux échantillons proviennent-ils d'une seule population de moyenne Mx ou proviennent-ils de deux populations distinctes de moyennes M1 et M2?

Cette analyse peut être réalisée par une ANOVA I à deux niveaux.

Les hypothèses:

Hypothèse nulle H0:

H0: M1 = M2 = Mx

les moyennes des échantillons appartiennent à une seule population de référence de moyenne Mx

Hypothèse alternative H1:

H1: M1 > M2 .

les moyennes des échantillons appartiennent à 2 populations distinctes. La population 1 a une moyenne M1 supérieure à la moyenne M2 de la population2

ou encore

H1: M1 < M2 .

les moyennes des échantillons appartiennent à 2 populations distinctes. La population 1 a une moyenne M1 inférieure à la moyenne M2 de la population2

ou encore

H1: M1 ≠ M2 .

les moyennes des échantillons appartiennent à 2 populations distinctes. La population 1 a une moyenne M1 différente de la moyenne M2 de la population2

 

Calculer la valeur observée:

Cas 1: les variances des populations 1 et 2 (VAR1 et VAR2) sont connues:

La réduction de la moyenne de l'échantillon peut se faire par le calcul d'une valeur de Z observé dont la formule est la suivante:

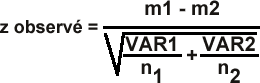
Où m1 et m2 sont les moyennes des 2 échantillons; VAR1 et VAR2 sont les variances des 2 populations 1 et 2; n₁ et n₂ sont les tailles respectives des échantillons 1 et 2.

Trouvez dans les tables de Z, la ou les valeurs seuil en tenant compte de alpha et de H1.

AH0 (et donc RH1)	Les échantillons de moyenne m1 et m2 appartiennent à une seule population de référence dont la moyenne est Mx
RH0 (et donc AH1)	Les échantillons de moyenne m1 et m2 n'appartiennent pas à la même population de référence dont la moyenne est Mx mais appartiennent à 2 populations distinctes dont les moyennes respectives M1 et M2 sont telles que M1 est plus grande OU plus petite OU différente par rapport à M2.

Cas 2: les variances des populations 1 et 2 (VAR1 et VAR2) sont inconnues:

Dans ce cas, il n'est plus possible de calculer directement une valeur de z observée car il nous manque les valeurs de variances des populations de référence VAR1 et VAR2.

Pour pouvoir comparer les moyennes des 2 échantillons, l'expérimentateur va devoir remplacer les variances des deux populations indépendantes par les variances estimées des 2 échantillons, var1 et var2.

Une question préalable doit être posée: La variabilité des 2 échantillons est-elle comparable, homogène? En d'autres termes, il faut vérifier l'égalité des variances des 2 populations étudiées, c'est-à-dire l'homoscédasticité. En effet si les variances sont hétérogènes, la différence de variance risque d'être confondue avec une différence de moyenne.

2.1 : Test sur l'homogénéité des variances des échantillons comparés:

Réalisation du test:

H0: var1 = var2	Les variances des populations comparées sont homogènes
Pour 2 variances : H1: var1 > var2 H2: var1 < var2	La variance 1 est plus grande que la variance 2 La variance 2 est plus grande que la variance 1
Pour réaliser ce test, l'expérimentateur établit le rapport Var max/Var min. Ce rapport est une valeur appelée F observé que l'on peut comparer avec une valeur F des tables de Fisher ( voir Module 125 : page 3 : Test de Fisher).
Fobservé = var1 / var2 si var1 plus grande que var2
L'expérimentateur va ensuite comparer cette valeur à une valeur théorique des tables de F de Fisher-Snedecor. Tester les hypothèses alternatives H1 et H2 en même temps implique la réalisation d'un test bidirectionnel. En général, ce test s'effectue avec une confiance de 95%. Ce test étant bidirectionnel, le seuil est fixé à alpha/2.
Fthéorique;(n1-1) dl; (n2-1)dl; 0,975	L'expérimentateur doit sélectionner la table où P(F < f) = 0,975. Les degrés de liberté du numérateur (n1-1)dl correspondent à ceux de l'échantillon dont la variance est la plus grande. Ils permettent de rentrer en tête de colonne dans la table. Les degrés de liberté du dénominateur (n2-1)dl correspondent à ceux de l'échantillon dont la variance est la plus petite. Ils permettent de rentrer en tête de ligne dans la table.
AH0 si Fobservé est plus petit que Fthéorique	Les variances des populations d'où sont issues les échantillons sont considérées comme homogènes et l'expérimentateur peut alors envisager de comparer les moyennes des populations d'où sont issus les échantillons.
RH0 si Fobservé est plus grand que Fthéorique	Les variances des populations d'où sont issues les échantillons sont considérées comme hétérogènes. Il est alors IMPOSSIBLE de comparer par la suite les moyennes pour des échantillons dont les variances ne sont pas homogènes. Dans de nombreux cas, une transformation X'=log(x) ou X'=racine(x) permet d'homogénéiser les variances.

2.2 :Test de comparaison des moyennes des populations d'où proviennent les 2 échantillons:

CONDITION: Ce test d'hypothèses portant sur les moyennes n'est possible QUE SI l'homogénéité des variances des populations a été confirmée par le test détaillé au point précédent

Les hypothèses H0 et H1 sont celles décrites plus haut.

L'expérimentateur va ensuite calculer une valeur de t observé: Dans cette formule, par rapport à celle du Z observé détaillée ci dessus, on remplacera VAR1 et VAR2 par une seule variance appelée "variance résiduelle" S_r² obtenue à partir des variances des deux échantillons var1 et var2.

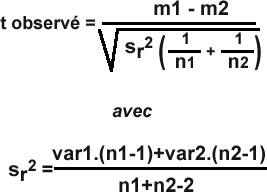
Où m1 et m2 sont les moyennes des 2 échantillons; S²_r est la variance résiduelle ; n₁ et n₂ sont les tailles respectives des échantillons 1 et 2, var1 et var2 sont les variances respectives des deux échantillons 1 et 2.

Ensuite, il reste à trouver dans les tables de t de Student (l'aspect de la courbe est aussi une courbe de Gauss), la ou les valeurs seuil en tenant compte de alpha et de H1. La valeur de t de Student nécessite aussi la détermination d'un certain nombre de degrés de liberté. Pour trouver la ou les valeurs seuil, il faut donc rechercher:

t_seuil;(n₁+n₂-2) degrés de liberté

Où "seuil" représente H1 (seuil peut être (1-α) ou α ou (1-α/2) ou (α/2)); n est la taille de l'échantillon.

AH0 (et donc RH1)	Les échantillons 1 et 2 appartiendraient, jusqu'à preuve du contraire, à la population de référence dont la moyenne est Mx.
RH0 (et donc AH1)	Les échantillons 1 et 2 n'appartiendraient pas à la population de référence dont la moyenne est Mx mais à deux autres populations dont les moyennes M1 et M2 sont plus grandes OU plus petites que celle de la population de référence.