L'analyse de la régression dans l'ANOVA est une méthode de calcul qui permet de découper la variabilité expliquée (factorielle) en deux parties:

1. La première partie contient la variabilité expliquée réellement par le modèle linéaire (SCEreg).
2. La seconde partie contient la variabilité expliquée par la non linéarité de la relation (SCEnl)

SCEF=SCEreg + SCEnl

Le principe de la régression dans l'ANOVA est de tester ces deux parties de la variabilité factorielle (variabilité due à la régression et variabilité non linéaire) par rapport à la variabilité résiduelle.

	SCE	dl	CM	F observé	F tables
TOTALE	SCET	N-1
Régression	SCEreg	1	CMreg	CMreg/CMR	Fdl reg; dlR; 0,95 ou 0,99
non linéaire	SCEnl	na-2	CMnl	CMnl/CMR	Fdl nl; dlR; 0,95 ou 0,99
RESIDUELLE	SCER	N-na	CMR

Test sur la régression :

Si le F observé pour la régression est supérieur au F des tables pour 1 dl (correspondant aux degrés de liberté de la variabilité due à la régression) et (N-na) dl (correspondant aux degrés de liberté de la variabilité résiduelle), cela signifie que lorsqu'on applique a priori le modèle linéaire µ_i=ß0+ß1X_i la pente ß1 est non nulle. Il y a donc une relation significative entre les deux paramètres étudiés (X et Y c'est-à-dire l'âge et la pression sanguine).

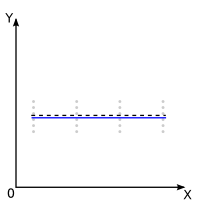
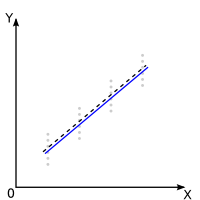
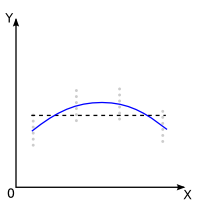
Dans les graphiques ci-dessous le résultat de ce test est symbolisé par la droite noire en pointillés. Lorsque le test est non-significatif la droite a une pente nulle, lorsqu'il est significatif, elle a une pente significative, illustré ici par une pente de 40 degrés en positif. Mais la pente pourrait très bien être négative. Pour le savoir, il faut se baser sur le signe de la SPE.

Test sur la non-linéarité :

Si le F observé pour l'aspect non linéaire est supérieur au F des tables pour (na-2)dl (correspondant aux degrés de liberté de la variabilité due à l'aspect non linéaire de la variabilité) et (N-na) dl (correspondant aux degrés de liberté de la variabilité résiduelle), cela signifie que la distribution des Y s'écarte significativement du modèle linéaire utilisé a priori, et que la relation entre X et Y doit donc être considérée comme non-linéaire.

Dans les graphiques ci-dessous, le résultat de ce test est symbolisé par le trait bleu. Lorsque le test est non significatif, cela signifie que l'équation de régression idéale est de type linéaire. Lorsque le test est significatif, cela signifie que l'équation mathématique caractérisant au mieux la distribution des points est de type non-linéaire.

Explication graphique :

		Régression: CMreg/CMR
		Non Significatif : La droite utilisée a priori a une pente nulle	Significatif : La droite utilisée a priori a une pente non nulle
Non linéarité: CMnl/CMR	Non Significatif : Il n'y a pas d'écarts significatifs par rapport à la droite utilisée a priori: le modèle idéal peut être considéré, a posteriori, comme linéaire.
	Significatif : Il y a des écarts significatifs par rapport à la droite utilisée a priori: le modèle idéal peut être considéré, a posteriori, comme non linéaire.

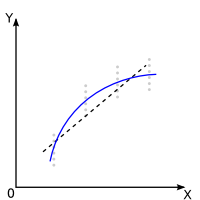Attention: Dans le cas de résultat significatif pour la non-linéarité, la courbe dessinée ici n'est qu'un des multiples exemples possibles. Dans ce cas l'étape suivante est de déterminer parmi tous les modèles non-linéaires (exponentiel, logarithmique, puissance, inverse, etc...) celui qui est le mieux adapté à la distribution des points.