Le centre de gravité du nuage de points est un point fictif qui a pour coordonnées (moyenne des X; moyenne des Y).

Pour chaque point, on peut quantifier son écart par rapport à ce centre de gravité en réalisant le calcul du produit des écarts:

PE=(X_i-M_x).(Y_i-M_y)

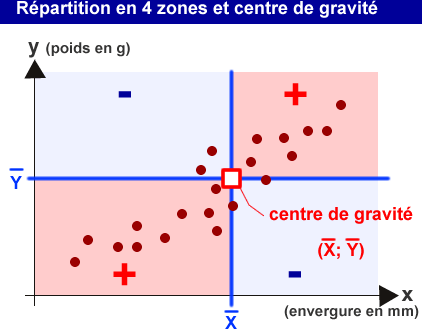
Ce produit des écarts est positif pour les points situés dans les quadrants roses du graphique ci-dessus, et négatif s'ils sont situés dans les quadrants bleus. Le nuage de points schématisé dans le graphique ci-dessus a donc des PE majoritairement positifs.

En réalisant la somme de tous ces PE, je peux donc avoir une estimation de l'orientation du nuage de points par rapport à son centre de gravité.

SPE : Somme des Produits des Ecarts

Si la SPE est positive, comme c'est le cas ici, le nuage de points est orienté de manière ascendante dans le sens gauche-droite. Si la SPE du nuage de points est négative, c'est qu'il est orienté de manière descendante.

La SPE amène donc énormément d'informations sur le sens de la relation qui pourrait éventuellement exister entre X et Y.

Note: Dans certaines situations expérimentales il peut être intéressant de comparer des nuages de points provenant d'expériences différentes. Dans ce cas, on doit ramener les deux nuages de points dans une échelle comparable. Pour cela on réalise une réduction des variables X et Y respectives, selon les formules suivantes:

X_réduit=(X_i-M_x)/S_x

Y_réduit=(Y_i.-M_y)/S_y

Le processus de réduction s'opère en retirant des coordonnées en X et en Y leur moyenne respective. Cela permet de repositionner les deux centres de gravité aux coordonnées identiques de (0;0).

Pour éliminer la variabilité propre au contexte expérimental, les différences entre coordonnées (X ou Y) expérimentales et moyennes (de X ou de Y) sont divisées par l'écart-type (de X ou de Y). Par définition, comme les centres de gravité sont aux coordonnées (0;0), la somme des valeurs réduites est nulle.