Les contenus sont © P. Calmant et E. Depiereux - 2004; G. Vincke B. De Hertogh et E. Depiereux 2008.
Imprimé le
12/3/2026
Une expérience fait parfois intervenir une série statistique à deux dimensions, c'est-à-dire 2 séries d'observations X et Y couplées. Lorsqu'au moins une des 2 variables est aléatoire, il est possible de considérer ces 2 variables simultanément au moyen d'une régression.
| 2 variables aléatoires | X = abondance d'une récolte (variable aléatoire) |
| Y = nombre de jours d'ensoleillement (variable aléatoire) | |
| 1 variable aléatoire et une variable contrôlée | X = température fixée (variable contrôlée) |
| Y = nombre de graines germées (variable aléatoire) |
Dans le cadre de ce cours, seul le cas où X est une variable contrôlée (non aléatoire, c'est-à-dire de valeurs fixées par l'expérimentateur) sera considéré.
Les valeurs prises par la variable X doivent être fixées sans erreur par l'expérimentateur.
X étant une variable contrôlée, on peut considérer Y comme fonction de X, mais pas le contraire :
Y=f(X)
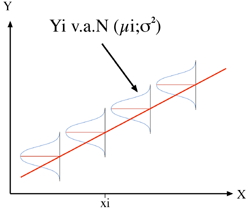
Pour chaque valeur Xi de X, il existe une population de valeurs Yi distribuée normalement, de moyenne µi et de variance σ2 homogène c'est-à-dire constante quelle que soit la valeur de X :
Yi v.a.N(µi; σ2)
Les moyennes µi correspondant aux valeurs Yi sont situées sur une droite dont les paramètres sont ß0 et ß1 telle que :
µi=ß0+ß1Xi
avec ß0 l'ordonnée à l'origine et ß1 la pente

Les variables aléatoires Yi sont indépendantes.
Supposons que l'on réalise une expérience portant sur l'étude de la pression sanguine (Y variable aléatoire) en fonction de l'âge (X variable contrôlée):
Lorsque l'âge des patients augmente, va-t-on observer un accroissement de leur pression sanguine?
Cet accroissement répond-il à un modèle linéaire?
| Age | 20 |
30 |
40 |
50 |
60 |
70 |
| valeurs | 120 |
123 |
134 |
130 |
142 |
145 |
125 |
120 |
128 |
137 |
136 |
138 |
|
121 |
126 |
127 |
135 |
139 |
141 |
|
118 |
125 |
131 |
133 |
141 |
148 |
Une simple analyse descriptive nous a permis les conclusions suivantes:
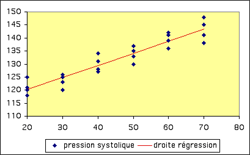
Pression systolique (Y aléatoire) en fonction de l'âge du patient (X fixe)
Une analyse de ce type reste assez simpliste et il n'est pas possible de savoir à coup sûr si la relation est bien linéaire! Pour cela il faut réaliser un test statistique sur la linéarité de la distribution, test que nous allons détailler à la page suivante.
L'analyse de la régression dans l'ANOVA est une méthode de calcul qui permet de découper la variabilité expliquée (factorielle) en deux parties:
SCEF=SCEreg + SCEnl
Le principe de la régression dans l'ANOVA est de tester ces deux parties de la variabilité factorielle (variabilité due à la régression et variabilité non linéaire) par rapport à la variabilité résiduelle.
| SCE | dl | CM | F observé | F tables | |
| TOTALE | SCET | N-1 | |||
| Régression | SCEreg | 1 | CMreg | CMreg/CMR | Fdl reg; dlR; 0,95 ou 0,99 |
| non linéaire | SCEnl | na-2 | CMnl | CMnl/CMR | Fdl nl; dlR; 0,95 ou 0,99 |
| RESIDUELLE | SCER | N-na | CMR |
Si le F observé pour la régression est supérieur au F des tables pour 1 dl (correspondant aux degrés de liberté de la variabilité due à la régression) et (N-na) dl (correspondant aux degrés de liberté de la variabilité résiduelle), cela signifie que lorsqu'on applique a priori le modèle linéaire µi=ß0+ß1Xi la pente ß1 est non nulle. Il y a donc une relation significative entre les deux paramètres étudiés (X et Y c'est-à-dire l'âge et la pression sanguine).
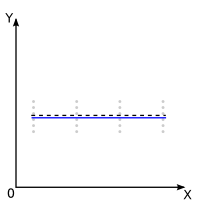
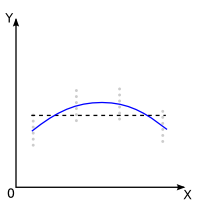
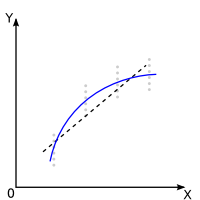
Dans les graphiques ci-dessous le résultat de ce test est symbolisé par la droite noire en pointillés. Lorsque le test est non-significatif la droite a une pente nulle, lorsqu'il est significatif, elle a une pente significative, illustré ici par une pente de 40 degrés en positif. Mais la pente pourrait très bien Ítre négative. Pour le savoir, il faut se baser sur le signe de la SPE.
Si le F observé pour l'aspect non linéaire est supérieur au F des tables pour (na-2)dl (correspondant aux degrés de liberté de la variabilité due à l'aspect non linéaire de la variabilité) et (N-na) dl (correspondant aux degrés de liberté de la variabilité résiduelle), cela signifie que la distribution des Y s'écarte significativement du modèle linéaire utilisé a priori, et que la relation entre X et Y doit donc être considérée comme non-linéaire.
Dans les graphiques ci-dessous, le résultat de ce test est symbolisé par le trait bleu. Lorsque le test est non significatif, cela signifie que l'équation de régression idéale est de type linéaire. Lorsque le test est significatif, cela signifie que l'équation mathématique caractérisant au mieux la distribution des points est de type non-linéaire.
| Régression: CMreg/CMR | |||
| Non Significatif : La droite utilisée a priori a une pente nulle |
Significatif : La droite utilisée a priori a une pente non nulle |
||
Non linéarité: |
Non Significatif : Il n'y a pas d'écarts significatifs par rapport à la droite utilisée a priori: le modèle idéal peut Ítre considéré, a posteriori, comme linéaire. |
 |
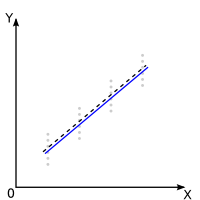 |
| Significatif : Il y a des écarts significatifs par rapport à la droite utilisée a priori: le modèle idéal peut Ítre considéré, a posteriori, comme non linéaire. |
 |
 |
|
Attention: Dans le cas de résultat significatif pour la non-linéarité, la courbe dessinée ici n'est qu'un des multiples exemples possibles. Dans ce cas l'étape suivante est de déterminer parmi tous les modèles non-linéaires (exponentiel, logarithmique, puissance, inverse, etc...) celui qui est le mieux adapté à la distribution des points.
En plus de ce tableau, il est nécessaire de calculer:
La somme des carrés d'écarts de la variabilité due à la régression se calcule de la manière suivante:
=SPE2 / SCEX
NB: Cette formule ne nécessite pas de demander le calcul en mode itératif ( "pomme+enter" sous mac, "ctrl+shift+enter" sous Windows) .
La somme des carrés d'écarts de la variabilité non linéaire se calcule de la manière suivante:
= SCEF - SCE reg
La somme des produits d'écarts se calcule de la manière suivante:
= SOMME((zone des X-moyenne des X)*(zone des Y-moyenne des Y))
NB: Cette formule nécessite de demander le calcul en mode itératif ( "pomme+enter" sous mac, "ctrl+shift+enter" sous Windows) !
La somme des carrés des écarts de X se calcule dans Excel de deux manières différentes:
1: Si pour chaque Xi correspond un série de Yij:
Votre tableau de données est alors organisé comme ceci:
|
X1
|
X2
|
X3
|
X4
|
|
Y11
|
Y21
|
Y31
|
Y31
|
|
Y12
|
Y22
|
Y32
|
Y32
|
|
...
|
...
|
...
|
...
|
Dans ce cas la formule à utiliser est : =ni*SOMME.CARRES.ECARTS(zone des X)
2: Si chaque Xi est répété à chaque ligne, et lui correspond un et un seul Y ij:
Votre tableau de données est alors organisé comme ceci:
Xi |
Yij |
X1 |
Y11 |
X1 |
Y12 |
X1 |
Y13 |
X1 |
Y14 |
X2 |
Y21 |
X2 |
Y22 |
... |
... |
Dans ce cas la formule à utiliser est : =SOMME.CARRES.ECARTS(zone des X)