Imaginons un modèle qui répartisse les observations en deux catégories, par exemple mâles et femelles, dans une population de sex-ratio 0.5

P(mâle)=1/3, P(femelle)=2/3; ratio=0.5

Comptons la fréquence des mâles et des femelles dans un échantillon (n=87) et la fréquence théorique attendue suivant la répartition 1/3, 2/3.

Calculons un écart quadratique entre les fréquences observées et théoriques, standardisé par la fréquence théorique :

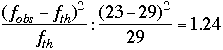
et rassemblons les valeurs dans un tableau :

	mâles	femelles	total
fi observée	23	64	87
fi théorique	29	58	87
écart quadratique standardisé	1.24	0.62	1.86

Fréquences observées et théoriques, écart quadratique, standardisé par la fréquence théorique, totaux.

Les fréquences observées fobs_i correspondent approximativement à la valeur de X=Po(m), expression dans laquelle m=n.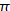 avec n la taille de l’échantillon et 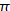la probabilité d’appartenir à la catégorie i.

La variance de cette fréquence observée est donc Var(X)= m=n.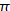

La quantité 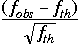est donc approximativement une variable Z(0 ;1).

L’écart global entre les observations et le modèle est calculé par la statistique :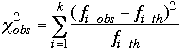

qui suit approximativement une distribution théorique

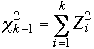
expression dans laquelle k représente le nombre de catégories et k-1 le nombre de degrés de liberté, dont dépend la forme de la courbe

Si l’on répète l’observation un grand nombre de fois, on obtiendra différentes fréquences, et différentes valeurs de obs

 

Echantillon N°	mâles	femelles	obs
2	29	62	0.0879
3	25	60	0.5882
4	25	73	2.6990
5	32	63	0.0053
6	37	66	0.3107
7	32	74	0.4717

Tableau -6 Répétition de l’expérience, fréquences observées et valeurs de obs

Comparons les valeurs obtenues pour obs avec k=2 :

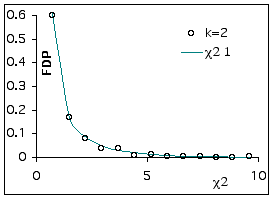
Figure -18 Comparaison des écarts quadratiques standardisés à la distribution théorique de khi-carré avec un degré de liberté.