Utilisation de la table de Z:

La table de Z (accessible depuis le lien "Tables" en haut de toutes les pages de ce site) vous donne les probabilités associées à des valeurs de z selon la relation p(Z<z).

Exemple : quelle est la probabilité d'être inférieur à un z de 1,96 dans une distribution de z v.a. N(0;1) ?
La table vous donne la réponse :
En tête de ligne on trouve la valeur entière et la première décimale de la valeur z.
En tête de colonne on trouve la seconde décimale de z.

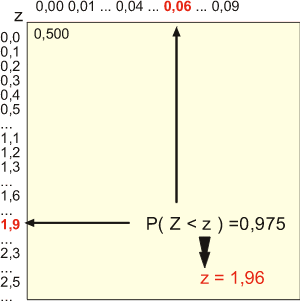
Donc P(Z<1,96)=0,975=97,5%

Inconvénient de la table de Z :

On peut la lire à l'envers donc par déduction on peut y trouver les valeurs de Z qui correspondent à une certaine probabilité.
Cependant toutes les probabilités intéressantes ne sont pas forcément représentées.
Si par exemple on cherche le z en dessous duquel il y a 98,5% des individus, on cherche la valeur 0,985 dans les valeurs du tableau, et en regardant les en-têtes de ligne et de colonne je trouve que le z qui correspond est 2,17 (ligne 2,1 et colonne 0,07).
Mais si je cherche le z tel que P(Z<z)=0,8=80%, il n'y a pas 0,8 dans les valeurs. On passe de 0,79955 à 0,80234, donc le z tel que P(Z<z)=0,8 est compris entre 0,84 et 0,85.

Cette table peut donc s'employer dans le sens :
z connu --> trouver la probabilité P(Z ≤ z)
ou dans le sens :
probabilité P(Z ≤ z) connue--> trouver le z correspondant, mais elle n'est pas pratique dans ce sens là.

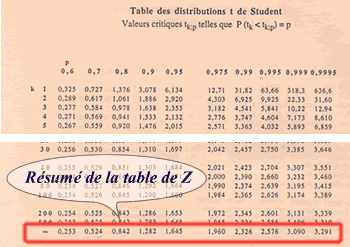
Utilisation de la table de Student :

La table de Student part des probabilités et donne les valeurs des variables réduites correspondantes (z ou t).
Si la variance de la population est connue (σ²), on peut employer la table de t de Student comme s'il s'agissait d'une table simplifiée de Z.
L'avantage d'une telle table est de pouvoir donner rapidement des valeurs de Z ou des probabilités très couramment utilisées dans les tests d'hypothèses (voir l'emploi des intervalles de confiance).

• En tête de colonne (p): donne la probabilité P(Z ≤ z)
• En tête de ligne (k): se positionner en l'"infini"

Dans notre exemple précédent :

P(Z<z)=0,8=80% donne ici directement une valeur exacte de 0,842.

En conclusion :

Pour trouver une probabilité à partir d'une valeur de z : on utilise la table de Z.

Pour trouver une valeur de z à partir d'une probabilité : on utilise la table de student, dernière ligne.