- équation et symbolique
- symétrie autour de la moyenne
- modification de la variance
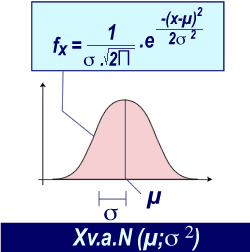
La distribution normale se caractérise par une équation
faisant intervenir la moyenne µ et la variance σ2.
Par convention, nous adopterons la convention d'écriture: X v.a.N(µ;
σ2)
. Dans la littérature, on peut aussi trouver: µ± σ ( moyenne ± écart-type).
| Symétrie
autour de la moyenne |
|
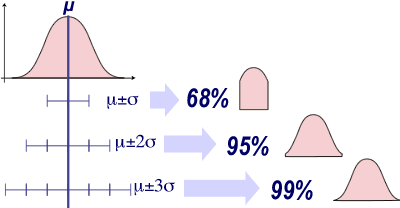
La courbe de Gauss-Laplace est symétrique:
- Lorsqu'on sélectionne l'intervalle compris entre +1 et -1
écart-type autour de la moyenne µ (de μ-σ jusque μ+σ), on isole 68% des individus
d'une population normale.
- Lorsqu'on sélectionne l'intervalle compris entre +2 et -2
écarts-types autour de la moyenne µ (de μ-2σ jusque μ+2σ), on isole 95% des individus
d'une population normale.
- Lorsqu'on sélectionne l'intervalle compris entre +3 et -3 écarts-types
autour de la moyenne µ (de μ-3σ jusque μ+3σ), on isole 99% des individus d'une population
normale.
| Modification
de la variance |
|
Lorsque la variance d'une population diminue, cela se traduit par une
dispersion moins importante de la courbe autour de la moyenne. Concomitamment,
le sommet de la courbe tend à s'élever afin de préserver
une surface totale sous la courbe égale à 1 (ou 100%).
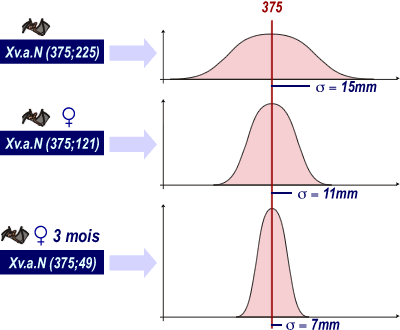
Exemple:
Dans une population de chauves-souris de l'espèce A, l'envergure
X est une v.a. N(375; 225)
Dans une population de chauves-souris de l'espèce A femelles, l'envergure
X est une v.a. N(375; 121)
Dans une population de chauves-souris de l'espèce A femelles de
3 mois, l'envergure X est une v.a. N(375; 49)
etc.
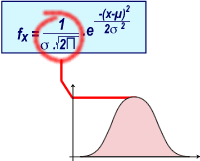
| Influence de la variance sur le sommet
de la courbe de Gauss:
Si la variance diminue, le sommet de la courbe tend à augmenter.
En effet, dans l'équation de la courbe, l'écart-type
se trouve au dénominateur(voir terme entouré en rouge).
Plus l'écart-type est petit, plus ce terme tend à
devenir grand...
|
 |
|