1. Dans une population donnée, la probabilité de trouver le gène Z actif est de 50%. Soit X le nombre de patients possédant ce gène Z actif. Une expérience a été menée sur un échantillon de 25 personnes (arrondir les réponses à deux décimales significatives).
- Quelle est la probabilité de déceler la présence d'un gène inactif chez 10 personnes au moins dans cette expérience?
solution: P(X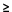 10) = 1-P(X 10) = 1-P(X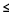 9)=1 - 0.1148= 0.89 9)=1 - 0.1148= 0.89
- Quelle est la probabilité de trouver 5 personnes possédant ce gène Z actif? Combien de combinaisons sont possibles?
solution: P(X=5) = P(X≤5)-P(X≤4)= 0,0020 - 0,0005 = 0,0015 ; 53 130 combinaisons possibles
2. Un examen de statistique rencontre un taux d'échec de 35%. Quelle est la probabilité que, sur 10 étudiants sélectionnés aléatoirement dans l'auditoire, il y ait:
- Plus de 2 étudiants en échec?
solution: P(X>2) = 0,74
- Plus de 5 étudiants en échec?
solution: P(X>5) = 0,095
3. Une rivière comporte une population d'écrevisses. Un écologiste réalise une expérience en disposant tous les 10 mètres une nasse à écrevisses. Il en place ainsi 25 et les numérote de 1 à 25. Sachant que pour cette rivière, il n'y a que 15% de chances de relever une nasse vide:
- Déterminer la probabilité de relever 3 nasses vides?
solution: P(X=3) = 0,22
- Si l'écologiste relève 2 nasses vides sur les 25, combien de combinaisons sont possibles?
solution : 300 combinaisons possibles
|

