Une étude est réalisée
sur une population de chauve-souris. L’envergure moyenne est, selon
des publications très sérieuses, de (375 ± 15) millimètres.
- De quel type de variable aléatoire parle-t-on ?
Définissez-la en employant la symbolique vue au cours
- Quel modèle doit-on associer à cette
variable aléatoire ? Aidez-vous du formulaire pour écrire
l’équation de ce modèle. Que vaut la densité
de probabilité au sommet de la fonction de probabilité du
modèle f(x) ?
- Dans cette population, déterminez les limites
inférieures et supérieures permettant de sélectionner,
autour de la moyenne, 68 % - 95 % - 99 % des individus
de la population ?
- Quelle proportion des individus possède
une envergure :
- Inférieure à 382,86 mm ?
- Inférieure à 378,795 mm ?
- Supérieure à 421,35 mm ?
- Une chauve-souris prélevée dans
cette population possède une envergure de 405 mm. Appartient-elle
à l’intervalle autour de la moyenne isolant 95 % des
individus de la population ? En est-il de même avec un individu
de 346 mm ?
- Que vaut approximativement (donnez une fourchette
de probabilités) la probabilité de trouver un individu dont
la taille serait inférieure à 405 mm ? Refaire l’exercice
pour un individu de moins de 346 mm ?
Exercice 2
La pression sanguine chez le rat
suit un modèle de Gauss-Laplace. Elle est de 120 mm de Mercure pour
une variance de 100 mm².
- De quel type de variable aléatoire
parle-t-on ? Définissez-la en employant la
symbolique vue au cours.
- Quelles sont les limites de pression sanguine
telles que la pression sanguine la plus petite de cette
zone est inférieure ou égale à 95 %
et la plus grande inférieure ou égale à
99 % ? Faites apparaître vos réponses
dans un tableau tel que :
| Si
s vaut : … mm |
Limite
inférieure |
Limite
supérieure |
| P(X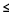 xi)=… xi)=…
|
Zi
vaut … |
|
|
- Déterminez les limites de l’intervalle
autour de moyenne permettant d’isoler 68 % ;
95 % et 99 % pour la population de chauves-souris
adultes mâles sachant que la pression sanguine moyenne
est aussi de 120 mais la variance est quatre fois moindre
par rapport à la variabilité de la population
prise dans sa totalité. Comme au point précédent,
réalisez un tableau pour résumer vos résultats.
Définissez symboliquement cette sous-population.
-
Lorsque la variance diminue, comme c’est
le cas dans cet exercice, comment évolue la fonction
f(x), notamment au niveau de la densité de probabilité
lorsque X = µ ? Comparez ces valeurs pour la population
totale de chauves-souris et la sous-population des mâles.
|

