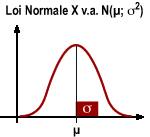
Cette distribution devient continue et se modélise par une courbe de Gauss-Laplace : c’est la variable aléatoire normale X v.a. N (µ ; σ²). La plupart des variables biologiques obéissent à un tel modèle. Il existe une moyenne et une variance propre à chaque variable, compliquant de ce fait le calcul des probabilités sous la courbe.

Afin de faciliter le calcul de probabilités, il est possible de créer une variable aléatoire normale dépourvue d’unités, centrée sur 0 et de variance 1 : c’est la variable aléatoire réduite Z [ Z v.a. N (0 ;1)]. Elle a été totalement caractérisée et les probabilités calculées pour un grand nombre d'intervalles z+Dz.

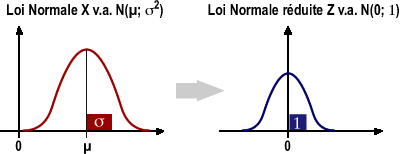
Une simple transformation d’une variable aléatoire normale X permet d'obtenir Z et donc d’évaluer rapidement les probabilités correspondantes. La conversion se fait par l’intermédiaire de la formule suivante :

zi = (xi-µ)/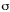