Table de contingence

Une table de contingence est un outil permettant de résoudre rapidement et facilement des problèmes de probabilités.

Une table de contingence est un tableau qui se présente ainsi :

	A	A*
B	p(A∩B)	p(A*∩B)	p(B)
B*	p(A∩B*)	p(A*∩B*)	p(B*)
	p(A)	P(A*)	1

Une table de contingence comprend donc toutes les probabilités d'évènements, ainsi que celles des intersections possibles entre évènements.

Le principe de calcul est que chaque cellule de fin de ligne ou de fin de colonne est la somme des deux cellules qui précèdent.
Ainsi, pour les lignes :
p(A∩B) + p(A*∩B) = p(B)
p(A∩B*) + p(A*∩B*) = p(B*)
p(A) + p(A*) = 1
Et pour les colonnes :
p(A∩B) + p(A∩B*) = p(A)
p(A*∩B) + p(A*∩B*) = p(A*)
p(B) + p(B*) = 1

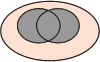
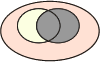
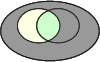
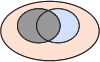
Pour bien comprendre les relations au sein d'une table de contingence, prenons les illustrations des diagrammes de Venn :

	A	A*
B	p(A∩B)	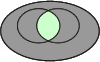p(A*∩B)	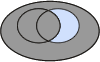p(B)
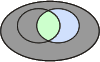B*	p(A∩B*)	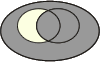p(A*∩B*)	p(B*)
	p(A)	p(A*)	1

Exemple de résolution d'exercice avec les tables de contingence

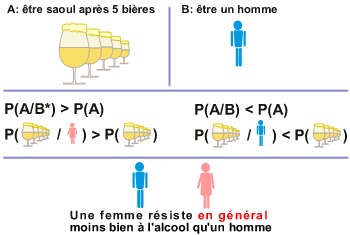
Soit une population comptant autant d'hommes que de femmes. On sait qu’il y a une chance sur deux d'être saoul après 5 bières. Un homme a 30% de chance d'être saoul après avoir bu 5 bières. Répondez aux questions suivantes :

1. La probabilité d'être saoul après 5 bières dépend-elle du sexe? (Justifiez numériquement votre réponse)
2. Quelle est la probabilité de ne pas être saoul après 5 bières ou d'être un homme?
3. Quelle est la probabilité d'être une femme et que celle-ci ne soit pas saoule après 5 bières?
4. Quelle est la probabilité de ne pas être saoule après 5 bières alors qu'on est une femme?
5. Quelle est la probabilité pour un homme de ne pas être saoul après 5 bières?

 

Traduction de l'énoncé et des questions:

Les événements de l'énoncé...	... et leurs contraires.
A = être saoul après 5 bières	A* = ne pas être saoul après 5 bières
B = être un homme	B* = être une femme

Les événements de l'énoncé... P(A/B) = 0,3 P(A) = 0,5 P(B) = 0,5

... et leurs contraires. P(A*/B) = 0,7 P(A*) = 0,5 P(B*) = 0,5

Les questions... P(A) = P(A/B) P(A*UB) P(A*∩B*) P(A*/B*) P(A*/B)

Table de contingence:

 

1) Entrer les données de l'énoncé:

	A	A*
B	0,15		0,5
B*			0,5
	0,5	0,5	1

Avec A (être saoul après 5 bières) et B (être un homme).

Postulats:

Les valeurs des événements entiers se retrouvent toujours en bout de ligne ou de colonne.

Les cases se trouvant à l'intersection d'une ligne et d'une colonne constituent des probabilités d'intersection.

La case en bas à droite représente l'union d'un événement et de son contraire. Soit 1 ou 100%.

Il est possible aussi de déterminer l'intersection entre A et B car nous connaissons P(B) et P(A/B):

P(A∩B)= P(B).P(A/B) = 0,5.0,3 =0,15

 

2) En déduire le reste du tableau:

 

	A	A*
B	0,15	0,35	0,5
B*	0,35	0,15	0,5
	0,5	0,5	1

 

Résolutions:

1) La probabilité d'être saoul après 5 bières dépend-elle du sexe? (Justifiez numériquement votre réponse)

P(A) = P(A/B)?

0,5 différent de 0,3

Le sexe influence la probabilité d'être saoul après 5 bières. Les deux événements sont donc dépendants.

 

2) Quelle est la probabilité de ne pas être saoul après 5 bières ou d'être un homme?

P(A*UB)?

P(A*UB) = P(A*) + P(B) - P(A*∩B) =0,5+0,5-0,35 = 0,65 ou 65%

 

3) Quelle est la probabilité d'être une femme et que celle-ci ne soit pas saoule après 5 bières?

P(A*∩B*)? = 0,15 ou 15%

 

4) Quelle est la probabilité de ne pas être saoule après 5 bières alors qu'on est une femme?

P(A*/B*)?

P(A*/B*)= P(A*∩B*) / P(B*) = 0,15 / 0,5 = 0,3 ou 30 %

 

5) Quelle est la probabilité pour un homme de ne pas être saoul après 5 bières?

P(A*/B) ?

P(A*/B) = 1 - P(A/B) = 1 - 0,3 = 0,7