Les contenus sont © P. Calmant et E. Depiereux - 2004; G. Vincke B. De Hertogh et E. Depiereux 2008.
Imprimé le
13/3/2026
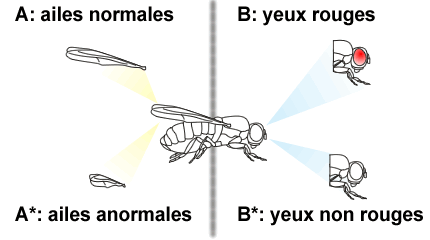
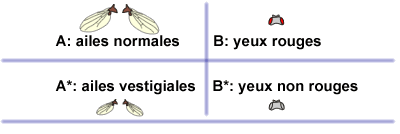
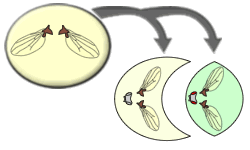
Par exemple imaginons d'étudier des drosophiles, et, plus particulièrement, la couleur des yeux et la taille des ailes.
Afin de simplifier les équations à venir, l'évènement "avoir des ailes normales" est noté A et l'évènement "avoir des yeux rouges" est noté B.
L'évènement A ("avoir des ailes normales") est opposé à A* c'est-à-dire "avoir des ailes anormales". De même, l'évènement contraire de B ("avoir des yeux rouges") est noté B* et représente le fait d'avoir "des yeux d'une autre couleur que rouge".

En pratique, si la probabilité d'avoir des ailes normales dans la population de drosophiles est de 30%, cela implique qu'il y a 70% des drosophiles qui ont des ailes différentes de la normale (courtes, courbées, doubles, etc.). On écrira alors:
P(A*) = 1-P(A)
P(A) = 0,3 et P(A*) = 0,7
Schématiquement, des événements peuvent être représentés sous la forme d'ensembles "emboîtés" les uns dans les autres pour former un diagramme de Venn.
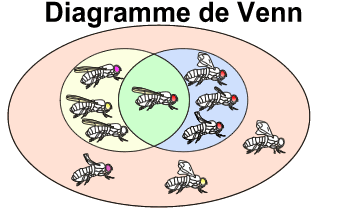
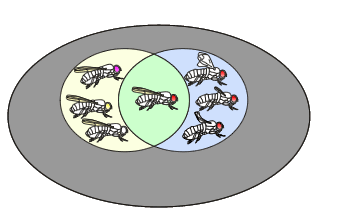
Soit l'étude porte sur les drosophiles. Dans la population de drosophiles (en rose), il existe des drosophiles avec des ailes normalement constituées et des drosophiles avec des yeux rouges.
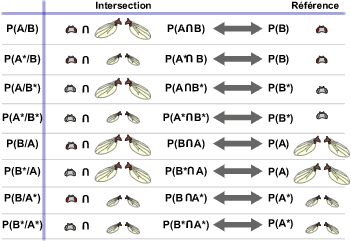
Dans le calcul des probabilités, les formules employées font apparaître les lettres: A et B. Nous utiliserons la convention suivante:
Dans une problématique donnée, le premier événement cité sera nommé A et le second B. Dans l'exemple, l'événement A est l'événement "avoir des ailes normales" et B "avoir des yeux rouges".
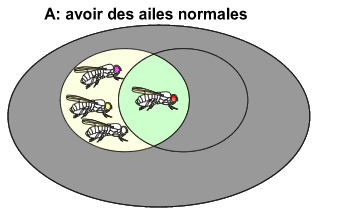
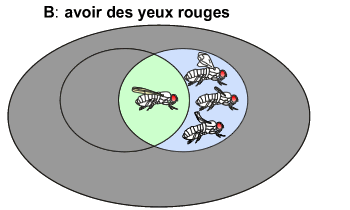
Par convention, le contraire d'un événement est désigné par la même lettre que l'événement avec une "*" à sa suite.
Ainsi, le contraire de l'événement A ("avoir des ailes normales") est l'événement A* ("avoir des ailes non normales"). Sur le diagramme de Venn, cet événement se représente comme suit:
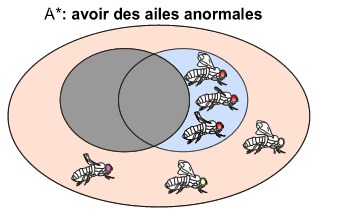
NB: l'événement A est représenté en grisé. Tout le reste (en couleur et montrant des drosophiles de morphologies variées) représente l'événement A*.
De même, le contraire de l'événement B ("avoir des yeux rouges") est l'événement B* ("avoir des yeux d'une autre couleur que rouge") et se représente comme suit:

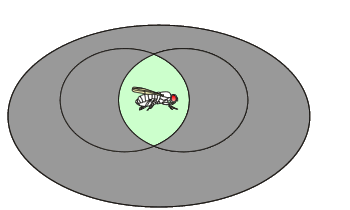
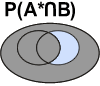
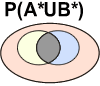
Lorsque deux événements se retrouvent simultanément sur un même individu, on parle d'intersection de ces deux événements. Ainsi, une drosophile qui possède des ailes normales (A) et des yeux rouges (B) est symbolisée de la manière suivante:
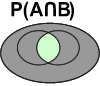
P(A∩B)
Dans le diagramme de Venn, cette probabilité se représente comme suit:
![]() Les zones grisées ne font pas partie de cette probabilité!
Les zones grisées ne font pas partie de cette probabilité!
 |
 |
|
 |
 |
|
|
P(A∩A*)=0
|
P(B∩B*)=0
|
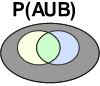
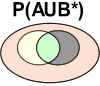
Le fait que deux événements peuvent se réaliser simultanément sur un même individu (intersection) ou seulement un seul (ou aucun) sur un individu s'appelle l'union de deux évènements. Ainsi, une drosophile qui possède des ailes normales (A) ou des yeux rouges (B) est symbolisée de la manière suivante:
P(AUB)
Dans le diagramme de Venn, cette probabilité se représente comme suit:
![]() Les zones grisées ne font pas partie de cette probabilité!
Les zones grisées ne font pas partie de cette probabilité!
Voici les différentes unions possibles:
 |  | |
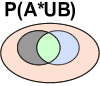 |  | |
| P(AUA*)
| P(BUB*)
|
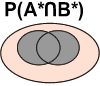
Le contraire d'une intersection entre deux événements est l'union des 2 événements contraires:
|
La probabilité d'intersection:
|
Son contraire:
|
 |
 |
 |
 |
 |
 |
 |
 |
|
P(A∩A*)=0
|
P(A*UA)=1
|
|
P(B∩B*)=0
|
P(B*UB)=1
|
![]() Les zones grisées ne font pas partie des probabilités énoncées
ci-dessus !
Les zones grisées ne font pas partie des probabilités énoncées
ci-dessus !
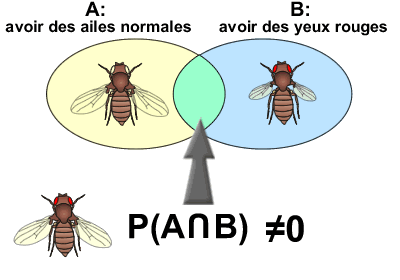
Soit l'événement A (avoir des ailes normales) et l'événement B (avoir des yeux rouges). S'il est possible de trouver des drosophiles avec des ailes normales ( P(A) ) ainsi que des drosophiles avec des yeux rouges ( P(B) ), il est aussi possible de trouver des drosophiles possédant à la fois des ailes normales et des yeux rouges.
Dans ce cas, la probabilité d'avoir des ailes normales ET des yeux rouges ( P(A∩B) ) est non nulle. On dira que les deux événements sont COMPATIBLES.
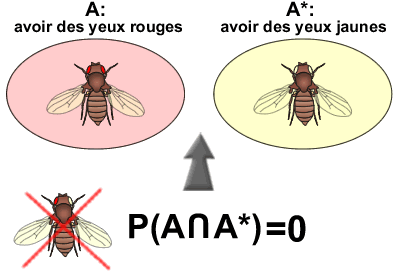
Soit l'événement A (avoir des yeux rouges) et l'événement A* (avoir, par exemple, des yeux jaunes). S'il est possible de trouver des drosophiles avec des yeux rouges ( P(A) ) ainsi que des drosophiles avec des yeux jaunes ( P(A*) ), il est par contre impossible de trouver des drosophiles possédant à la fois un oeil rouge et un oeil jaune.
Dans ce cas, la probabilité d'avoir des yeux rouges ET des yeux jaunes ( P(A∩A*) ) est nulle. On dira que les deux événements sont INCOMPATIBLES.
Soit une pièce de monnaie équilibrée. Lorsqu'on la lance en l'air, elle ne peut retomber que sur le côté "pile" ou sur le côté "face": P(pile) = 0,5


|
|
10 PREMIERS LANCERS: Sur 10 lancers, on peut obtenir, par chance, 10 fois la face PILE. |
P(PILE)10 = 0,000976...
|
|
|
11ème LANCER: Au 11ème lancer, la chance de faire un "pile" ou de faire un "face" est toujours la même, c'est-à-dire 1 chance sur 2 (0,5). La probabilité de faire un FACE au 11ème lancer ne dépend pas du fait qu'on ait fait un PILE aux 10 premiers lancers. On dira que les deux événements sont INDÉPENDANTS. |
P(FACE/PILE) =P(PILE) =P(FACE) = 0,5 |
NOMENCLATURE:
1. P(FACE / PILE) est une probabilité conditionnelle. Elle peut se traduire de la manière suivante:
|
P
|
(FACE
|
/
|
PILE)
|
|
Probabilité de |
faire un face au second lancer
|
Sachant que Dans le contexte de |
ait fait un pile au premier lancer
|
2. D'une manière générale, lorsque l'on dispose de 2 événements A et B indépendants, alors:
| P(A/B) = P(A) et P(B/A) = P(B) |
2. Dépendance:
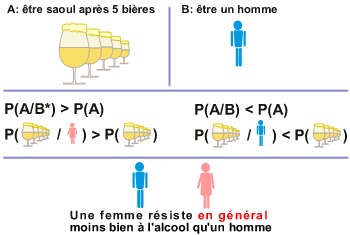
Comparons les hommes et les femmes par rapport à la consommation d'alcool.
Soit P(A) la probabilité d'être une femme et P(B) la probabilité d'avoir un taux d'alcoolémie > 0,5g/l après 3 bières.
Biochimiquement, il a été prouvé que les hommes résistent mieux à l'alcool que les femmes.
Cela implique que:
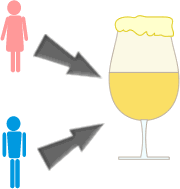 |
P(B/A) > P(B) |
La probabilité d'être
saoul sachant qu'on
est une femme est différente
de la probabilité d'être saoul
|
|
P(B/A*) < P(B) |
La probabilité d'être
saoul sachant qu'on
est un homme est différente
de la probabilité d'être saoul
|
NOMENCLATURE:
D'une manière générale, lorsque l'on dispose de 2 événements A et B dépendants, alors:
|
P(A/B) ≠ P(A) et P(B/A) ≠ P(B) |
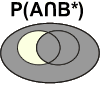
Supposons que les événements A (avoir des ailes normales) et B (avoir des yeux rouges) soient compatibles : P(A∩B) différent de 0.
Lorsque l'on souhaite connaître la proportion de drosophiles aux yeux rouges parmi les drosophiles aux ailes normales, on va donc étudier la probabilité P(B/A).
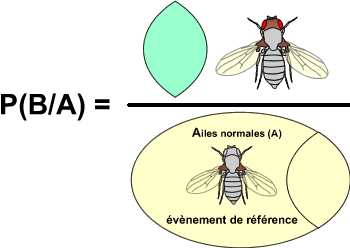
C'est-à-dire, en termes mathématiques:
| Pour décomposer une probabilité conditionnelle, il suffit de mettre au numérateur l'intersection entre les deux événements apparaissant dans la probabilité conditionnelle et au dénominateur la probabilité de l'événement de référence. |
Différents types de probabilités conditionnelles:
 |
 |
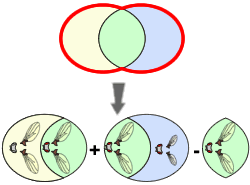
Cette loi permet de décomposer la probabilité d'une union en une série d'autres probabilités.
P(AUB) = P(A) + P(B) - P(A∩B) |
Ainsi, la probabilité de trouver des drosophiles aux ailes normales (A) ou des drosophiles aux yeux rouges (B) peut se décomposer de la façon suivante:
 |
|
En d’autres termes, la probabilité de trouver des drosophiles avec des ailes normales OU des yeux rouges s’obtient en additionnant la probabilité d’avoir des ailes normales quelle que soit la couleur des yeux à la probabilité d’avoir des yeux rouges quelles que soient les ailes (normales ou non) des drosophiles. À ce résultat, il faut cependant retirer la probabilité d’observer simultanément les drosophiles ayant à la fois les ailes normales et les yeux rouges (P(A∩B)) car cet événement se retrouve inclus à la fois dans l’ensemble A et dans l’ensemble B. Il est donc comptabilisé deux fois, d’où la nécessité de le retirer une fois pour éviter les doublons. Décomposition des probabilités d'union suivant la loi des probabilités totales: |
| P(AUB)= | P(A) + P(B) - P(A∩B) |
| P(AUB*)= | P(A) + P(B*) - P(A∩B*) |
| P(A*UB)= | P(A*) + P(B) - P(A*∩B) |
| P(A*UB*)= | P(A*) + P(B*) - P(A*∩B*) |
Cette loi permet de décomposer une probabilité d'intersection entre deux événements, en un produit de probabilités.
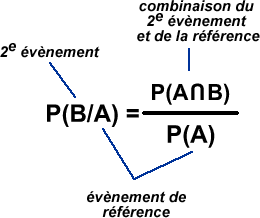
| P(A∩B) | =P(A).P(B/A) |
| =P(B).P(A/B) |
Cette loi est basée sur de la notion de probabilité conditionnelle vue précédemment...

C'est-à-dire, en termes mathématiques:

Comme la probabilité d'une intersection se retrouve à la fois dans la zone de l'événement A et de l'événement B, il est possible de comparer cette interaction par rapport à un de ces événements
| P(A∩B) | =P(A).P(B/A) | =P(B).P(A/B) |
| P(A∩B*) | =P(A).P(B*/A) | =P(B*).P(A/B*) |
| P(A*∩B) | =P(A*).P(B/A*) | =P(B).P(A*/B) |
| P(A*∩B*) | =P(A*).P(B*/A*) | =P(B*).P(A*/B*) |
|
Pour décomposer une probabilité d'intersection, écrivez la probabilité d'un événement seul (la référence), puis, écrivez "multiplié" et enfin, inscrivez la probabilité conditionnelle P(autre événement / événement de référence): |
|
|
P(réf. ∩ autre év.) = P(réf.).P(autre év. / réf.) |
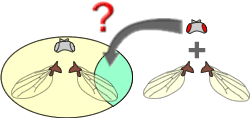
Un évènement complet peut être décomposé en deux intersections:
|
P(A)=P(A∩B)
+ P(A∩B*)
|
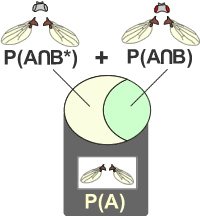
La probabilité d'avoir des ailes normales (A) regroupe les drosophiles aux ailes normales (A) et aux yeux non rouges (B*) ainsi que les drosophiles aux ailes normales (A) et aux yeux rouges (B).
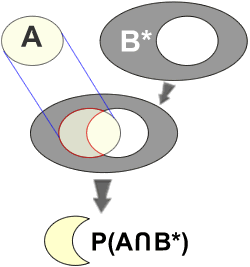
L'obtention de la probabilité de trouver des drosophiles aux ailes normales (A) et aux yeux non rouges (B*) peut être comme suit:
La superposition de l'évènement A et de l'évènement B* permet de mettre en évidence une zone de recouvrement commune aux deux évènements A et B*.
|
Pour décomposer une probabilité
d'un évènement (par exemple A) en une somme d'intersections: |
|
|
P(A)=P(A∩B)+P(A∩B*)
|
P(A)= |
P(A∩B)+P(A∩B*) |
P(A*)= |
P(A*∩B)+P(A*∩B*) |
P(B)= |
P(A∩B)+P(A*∩B) |
P(B*)= |
P(A∩B*)+P(A*∩B*) |
Une table de contingence est un outil permettant de résoudre rapidement et facilement des problèmes de probabilités.
Une table de contingence est un tableau qui se présente ainsi :
Une table de contingence comprend donc toutes les probabilités d'évènements, ainsi que celles des intersections possibles entre évènements.
Le principe de calcul est que chaque cellule de fin de ligne ou de fin de colonne est la somme des deux cellules qui précèdent.
Ainsi, pour les lignes :
p(A∩B) + p(A*∩B) = p(B)
p(A∩B*) + p(A*∩B*) = p(B*)
p(A) + p(A*) = 1
Et pour les colonnes :
p(A∩B) + p(A∩B*) = p(A)
p(A*∩B) + p(A*∩B*) = p(A*)
p(B) + p(B*) = 1
Pour bien comprendre les relations au sein d'une table de contingence, prenons les illustrations des diagrammes de Venn :
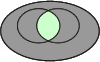 |
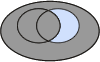 |
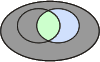 |
|
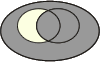 |
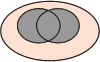 |
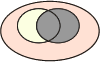 |
|
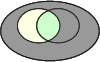 |
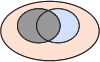 |
 |
Soit une population comptant autant d'hommes que de femmes. On sait qu’il y a une chance sur deux d'être saoul après 5 bières. Un homme a 30% de chance d'être saoul après avoir bu 5 bières. Répondez aux questions suivantes :
Traduction de l'énoncé et des questions:
| Les événements de l'énoncé... |
... et leurs contraires. |
| A = être saoul après 5 bières |
A* = ne pas être saoul après 5 bières |
| B = être un homme |
B* = être une femme |
| Les événements de l'énoncé... P(A/B) = 0,3 P(A) = 0,5 P(B) = 0,5 |
... et leurs contraires. P(A*/B) = 0,7 P(A*) = 0,5 P(B*) = 0,5 |
| Les questions...
|
1) Entrer les données de l'énoncé:
| |
|
||
| |
|
|
|
| |
|
||
| |
|
|
Avec A (être saoul après 5 bières) et B (être un homme).
Il est possible aussi de déterminer
l'intersection entre A et B car nous connaissons P(B) et P(A/B):
P(A∩B)= P(B).P(A/B) = 0,5.0,3 =0,15
2) En déduire le reste du tableau:
| |
|
||
| |
|
|
|
| |
|
|
|
| |
|
|
Résolutions:
1) La probabilité d'être saoul après 5 bières dépend-elle du sexe? (Justifiez numériquement votre réponse)
P(A) = P(A/B)?
0,5 différent de 0,3
Le sexe influence la probabilité d'être saoul après 5 bières. Les deux événements sont donc dépendants.
2) Quelle est la probabilité de ne pas être saoul après 5 bières ou d'être un homme?
P(A*UB)?
P(A*UB) = P(A*) + P(B) - P(A*∩B) =0,5+0,5-0,35 = 0,65 ou 65%
3) Quelle est la probabilité d'être une femme et que celle-ci ne soit pas saoule après 5 bières?
P(A*∩B*)? = 0,15 ou 15%
4) Quelle est la probabilité de ne pas être saoule après 5 bières alors qu'on est une femme?
P(A*/B*)?
P(A*/B*)= P(A*∩B*) / P(B*) = 0,15 / 0,5 = 0,3 ou 30 %
5) Quelle est la probabilité pour un homme de ne pas être saoul après 5 bières?
P(A*/B) ?
P(A*/B) = 1 - P(A/B) = 1 - 0,3 = 0,7
1. Une certaine réaction permet de détecter la présence d’une substance dans des prélèvements d’eau.
Lorsque la substance est présente, la réaction est positive dans 90% des cas.
Lorsque la substance est absente, la réaction est toujours négative.
Quelle est la probabilité que la substance soit présente, lorsque la réaction est positive ? La probabilité d’avoir la substance dans un prélèvement étant de 25%. P = 1.
2. La probabilité d’être de sexe masculin est de 0,5. La probabilité qu’un individu de sexe masculin soit de groupe sanguin A est de 0,40. La probabilité d’être d’un autre groupe sanguin que A est de 0,60.
- Quelle est la probabilité d’être une femme de groupe sanguin A ? P = 0,20
- Quelle est la probabilité d’être du groupe sanguin A ? P = 0,40
- Quelle est la probabilité qu’un individu de groupe sanguin A soit de sexe masculin ? P = 0,50.
3. Les eaux peuvent être polluées par la présence d’une bactérie A ou par celle d’une bactérie B. On a constaté la présence de A dans 20% des prélèvements et la présence de B dans 10% des prélèvements, 75% étant exempts de bactéries. Quelle est la probabilité qu’un prélèvement contaminé par B soit également contaminé par A ? P = 0,50.
4. Parmi les enfants traités par un vaccin anti-grippe, 20% ont fait une poussée grippale durant les 2 mois qui ont suivi l’administration du vaccin. Durant la même période, parmi les enfants non traités, 46% des enfants ont fait une poussée grippale. Quelle est la probabilité d’être grippé sachant qu’un enfant sur quatre reçoit le vaccin ? P = 0,395
5. Considérons une population de drosophiles.
La probabilité d’avoir une drosophile de grande taille est de 0,29. La probabilité d’avoir une drosophile avec des yeux blancs est de 0,13. Il y a indépendance entre la taille et la couleur des yeux.
- Quelle est la probabilité qu’une drosophile ait des yeux rouges sachant qu’elle est de petite taille ? P= 0,87
- Si on prend une drosophile au hasard, quelle est la probabilité qu’elle soit de petite taille et avec des yeux blancs ? P=0,0923
- Quelle est la probabilité qu’une drosophile aux yeux rouges soit de grande taille ? P = 0,29
- Si on prend une drosophile au hasard, quelle est la probabilité qu’elle ait des yeux rouges ou des yeux blancs ? P = 1
6. Lorsqu’une substance est présente dans l’eau, une certaine réaction permet de la détecter. On dira que la réaction est positive. La probabilité d’avoir un prélèvement sans la substance et positif est de 0,003. La probabilité d’avoir un prélèvement sans la substance et négatif est de 0,297. La probabilité d’avoir un prélèvement positif est de 0,528.
- Si on prend un prélèvement au hasard, quelle est la probabilité qu’il soit contaminé par la substance et négatif ? P = 0,175
- On prend un prélèvement au hasard, il est contaminé par la substance, quelle est la probabilité qu’il soit négatif ? P = 0,25
- Si on prend un prélèvement au hasard, quelle est la probabilité qu’il ne contienne pas la substance et que la réaction soit négative ? P = 0,297
- Si on prend un prélèvement au hasard, quelle est la probabilité qu’il soit contaminé par la substance et positif, ou qu’il soit positif ? P = 0,528
7. Un test pour détecter le cancer a été mis au point. La probabilité d’avoir un individu en bonne santé et positif au test est de 0,05. La probabilité d’avoir un individu atteint du cancer et positif au test est de 0,15. La probabilité d’avoir un individu en bonne santé est de 0,5.
- Si on prend un individu au hasard, quelle est la probabilité qu’il soit négatif au test ? P = 0,8
- Si on prend un individu au hasard, quelle est la probabilité qu’il soit en bonne santé et positif au test, ou qu’il soit positif au test ? P = 0,2
- Un individu est négatif au test, quelle est la probabilité qu’il soit en bonne santé ? P=0,5625
-Si on prend un individu au hasard, quelle est la probabilité qu’il soit atteint du cancer et négatif au test ?
P = 0,35
- Quelle est la probabilité qu’un individu soit atteint du cancer sachant qu’il est négatif au test ? P=0,4375
8. Des cultures de tissus peuvent être infectées par des bactéries ou par des champignons. La probabilité d’avoir une culture infectée par des champignons est de 0,4152. La probabilité d’avoir une culture sans bactéries est de 0,93. La probabilité d’avoir une culture infectée par des bactéries et par des champignons est de 0,0525.
- Si on prend une culture au hasard, quelle est la probabilité qu’elle soit infectée par des bactéries? P=0,07
- Y a-t-il indépendance entre infection par bactéries et infection par champignons ? non- Si on prend une culture au hasard, quelle est la probabilité qu’elle soit sans bactéries et sans champignons ? P= 0,5673
- Si on prend une culture au hasard, quelle est la probabilité qu’elle soit infectée par des bactéries et sans champignons ? P = 0,0175
 |
LOI DES PROBABILITÉS TOTALES: P(AUB) = P(A) + P(B) -P(A∩B) |
 |
LOI DES PROBABILITÉS COMPOSÉES: P(A∩B) = P(A).P(B/A) P(A∩B) = P(B).P(A/B)
|
|
SI A et B indépendants: P(A∩B) = P(A).P(B) |
|
 |
FORMULE HYBRIDE: P(A) = P(A∩B) +P(A∩B*) |