Cette loi permet de décomposer une probabilité d'intersection
entre deux événements, en un produit de probabilités.
| P(A∩B) |
=P(A).P(B/A) |
| =P(B).P(A/B) |
Cette loi est basée sur de la notion de probabilité conditionnelle
vue précédemment...
C'est-à-dire, en termes mathématiques:
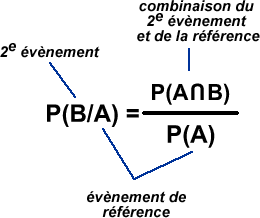
Comme la probabilité d'une intersection se retrouve
à la fois dans la zone de l'événement A et de l'événement
B, il est possible de comparer cette interaction par rapport à
un de ces événements
Décomposition des probabilités d'intersection
suivant la loi des probabilités composées:
| P(A∩B) |
=P(A).P(B/A) |
=P(B).P(A/B) |
| P(A∩B*) |
=P(A).P(B*/A) |
=P(B*).P(A/B*) |
| P(A*∩B) |
=P(A*).P(B/A*) |
=P(B).P(A*/B) |
| P(A*∩B*) |
=P(A*).P(B*/A*) |
=P(B*).P(A*/B*) |
 |
Pour décomposer une probabilité d'intersection,
écrivez la probabilité d'un événement
seul (la référence), puis, écrivez "multiplié"
et enfin, inscrivez la probabilité conditionnelle P(autre
événement / événement de référence):
|
P(réf. ∩ autre
év.) = P(réf.).P(autre
év. / réf.)
|
|

