Cette loi permet de décomposer la probabilité d'une union en une série d'autres probabilités.
P(AUB) = P(A) + P(B) - P(A∩B) |
Ainsi, la probabilité de trouver des drosophiles aux ailes normales (A) ou des drosophiles aux yeux rouges (B) peut se décomposer de la façon suivante: | |
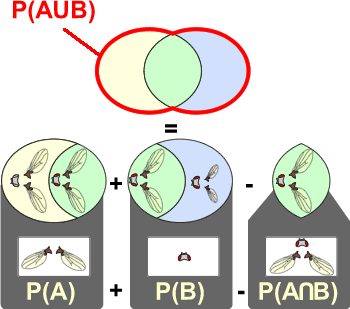
En d’autres termes, la probabilité de
trouver des drosophiles avec des ailes normales OU des yeux rouges
s’obtient en additionnant la probabilité d’avoir
des ailes normales quelle que soit la couleur des yeux à
la probabilité d’avoir des yeux rouges quelles que
soient les ailes (normales ou non) des drosophiles. À ce
résultat, il faut cependant retirer la probabilité
d’observer simultanément les drosophiles ayant à
la fois les ailes normales et les yeux rouges (P(A∩B)) car cet événement se retrouve inclus à
la fois dans l’ensemble A et dans l’ensemble B. Il est
donc comptabilisé deux fois, d’où la nécessité
de le retirer une fois pour éviter les doublons.
Décomposition des probabilités d'union suivant la
loi des probabilités totales:
|
| P(AUB)= |
P(A) + P(B) - P(A∩B) |
| P(AUB*)= |
P(A) + P(B*) - P(A∩B*) |
| P(A*UB)= |
P(A*) + P(B) - P(A*∩B) |
| P(A*UB*)= |
P(A*) + P(B*) - P(A*∩B*) |
|

