Le but de la régression simple est de déterminer le modèle mathématique qui permet d'expliquer au mieux la variabilité d'une variable Y en fonction d'une variable X.
Exemple: expliquer la variabilité de la taille de truites adultes (Y) en fonction de la température des bassins d'élevage (X).
Pour bien conceptualiser la démarche effectuée lors de l'analyse de la régression, prenons le problème à l'envers, et tentons de comprendre quels sont les fondements théoriques de cette analyse.
Pour cela, partons du modèle linéaire et tentons d'expliquer la manière dont des points peuvent se distribuer expérimentalement.
| Rappel : Régression linéaire simple: Une variable aléatoire X. Modèle : Y=B0+B1X |
Le modèle idéal d'une régression linéaire simple est une droite dans un plan.
Prenons un exemple ou Y=2+0,6X. |
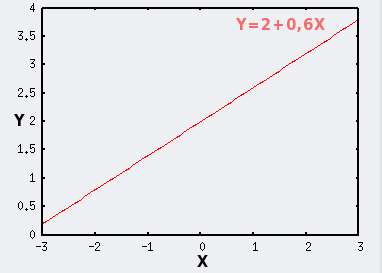 |
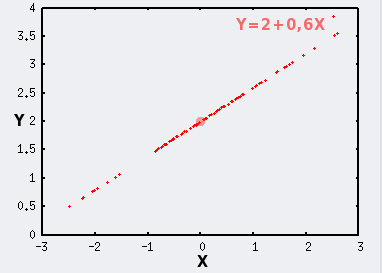
Lorsque X est une variable aléatoire normale, les points se projettent sur la trajectoire de la droite selon une distribution normale, et sont donc d'autant plus nombreux qu'on se rapproche du point dont les coordonnées sont (mX;mY).
La distribution des points sur la droite est donc influencée par le mode de distribution des X, c'est à dire par une variabilité de type horizontal.
Dans notre exemple X est une variable normale de paramètres μ=0 et σ=1.
Le point de coordonnées (mX;mY) est symbolisé par le gros point rouge.
|
 |
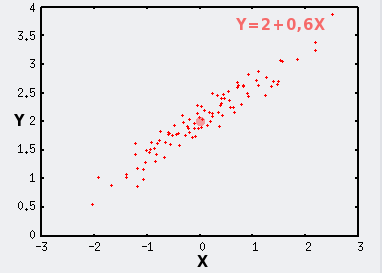
En conditions expérimentales, la distribution n'est jamais idéale. Des erreurs de mesures, des imprécisions, et des sources de variabilité d'origines diverses viennent s'ajouter au modèle normal. Dans ce cas les points ne se distribuent plus selon une droite parfaite, mais selon un nuage, d'autant plus proche de la droite parfaite que ces variabilités supplémentaires sont faibles.
Ces sources supplémentaires de variabilité, si X et Y sont mesurés, influencent la distribution des points horizontalement si elles s'appliquent à X, et verticalement si elles concernent Y.
Dans notre exemple, pour simplifier les choses, nous avons résumé ces sources de variabilité supplémentaires en une variable aléatoire qui disperse les points verticalement autour de la droite selon un modèle normal de paramètres ?=0 et ?=0,15.
Le point de coordonnées (mX;mY) est symbolisé par le gros point rouge.
|
 |
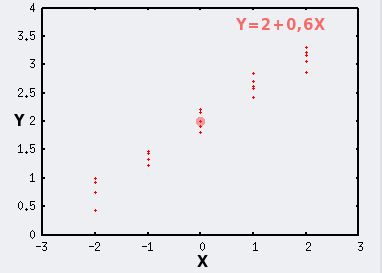
Lorsque la variable X est fixée, ici aux valeurs -2, -1, 0, 1 et 2, il n'y a plus de variabilité additionnelle sur X, et on visualise mieux la variabilité additionnelle qui ne concerne que Y, qui est toujours ici de paramètres μ=0 et σ=0,15.
Le point de coordonnées (mX;mY) est symbolisé par le gros point rouge.
|
 |
|
Le but de la régression est donc, face à une situation expérimentale, de chercher à quantifier ces sources de variabilités additionnelles verticales et horizontales, de manière à retrouver quel serait le modèle mathématique qui caractériserait au mieux la distribution des points si ces variabilités additionnelles, inévitables en conditions expérimentales, n'existaient pas.
|
Rappels :
Pour en savoir plus sur les modes de calculs de la pente et de l'ordonnée à l'origine :
|

