Module 230:

La régression multiple est la suite logique de la régression simple vue lors des statistiques descriptives à deux dimensions et dans l'ANOVA1.

Le but de la régression multiple est de déterminer le modèle mathématique permettant d’expliquer au mieux la variabilité d’une variable Y en fonction, non plus de une, mais de plusieurs variables X₁, X₂, X₃ etc...

Exemple: expliquer la variabilité de la taille de truites adultes (Y) en fonction de la température des bassins d'élevage (X₁), du pH de l'eau (X₂), de la teneur en protéines de leurs aliments (X₃), etc... le tout simultanément.

Tout comme pour la régression simple, il existe plusieurs modèles de régressions multiples:

Le modèle linéaire est une équation qui oriente une droite dans un hyper-espace qui a autant de dimensions qu'il y a de variables ( Y, X₁, X₂, X₃ = 4 dimensions). C'est le modèle de régression multiple le plus simple :

Y = B₀ + B₁X₁ + B₂X₂ + B₃X₃ + ...

Le terme B₀ est l'ordonnée à l'origine, c'est-à-dire la valeur de Y lorsque toutes les variables X_i sont nulles.

Les modèles non-linéaires (exponentiels, logarithmiques, etc...) sont très complexes, et sortent du cadre de ce cours. Ils ne seront donc pas abordés.

Cas particulier :

Le modèle polynomial est un modèle de régression simple car il ne concerne que deux variables (X et Y) mais qui sera néanmoins détaillé ici car son mode de calcul est similaire à celui de la régression multiple.

Le modèle polynomial ne concerne qu'une seule variable X, mais qui sera élevé à plusieurs puissances croissantes. Cette équation permet de tracer une courbe qui aura autant de points d’inflexion qu’il y a de degrés au polynôme :

Y = B₀ + B₁X + B₂X² + B₃X³ + ....

Le but de la régression simple est de déterminer le modèle mathématique qui permet d'expliquer au mieux la variabilité d'une variable Y en fonction d'une variable X.

Exemple: expliquer la variabilité de la taille de truites adultes (Y) en fonction de la température des bassins d'élevage (X).

Pour bien conceptualiser la démarche effectuée lors de l'analyse de la régression, prenons le problème à l'envers, et tentons de comprendre quels sont les fondements théoriques de cette analyse.

Pour cela, partons du modèle linéaire et tentons d'expliquer la manière dont des points peuvent se distribuer expérimentalement.

Rappel : Régression linéaire simple: Une variable aléatoire X. Modèle : Y=B0+B1X
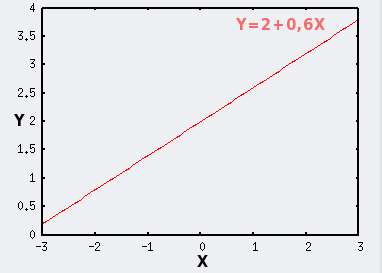
Le modèle idéal d'une régression linéaire simple est une droite dans un plan. Prenons un exemple ou Y=2+0,6X.
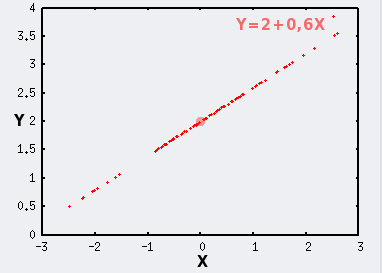
Lorsque X est une variable aléatoire normale, les points se projettent sur la trajectoire de la droite selon une distribution normale, et sont donc d'autant plus nombreux qu'on se rapproche du point dont les coordonnées sont (mX;mY). La distribution des points sur la droite est donc influencée par le mode de distribution des X, c'est à dire par une variabilité de type horizontal. Dans notre exemple X est une variable normale de paramètres μ=0 et σ=1. Le point de coordonnées (mX;mY) est symbolisé par le gros point rouge.
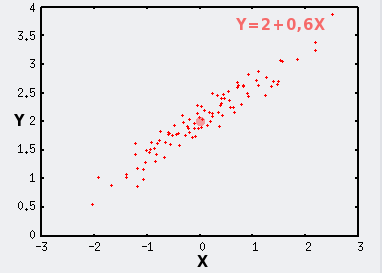
En conditions expérimentales, la distribution n'est jamais idéale. Des erreurs de mesures, des imprécisions, et des sources de variabilité d'origines diverses viennent s'ajouter au modèle normal. Dans ce cas les points ne se distribuent plus selon une droite parfaite, mais selon un nuage, d'autant plus proche de la droite parfaite que ces variabilités supplémentaires sont faibles. Ces sources supplémentaires de variabilité, si X et Y sont mesurés, influencent la distribution des points horizontalement si elles s'appliquent à X, et verticalement si elles concernent Y. Dans notre exemple, pour simplifier les choses, nous avons résumé ces sources de variabilité supplémentaires en une variable aléatoire qui disperse les points verticalement autour de la droite selon un modèle normal de paramètres ?=0 et ?=0,15. Le point de coordonnées (mX;mY) est symbolisé par le gros point rouge.
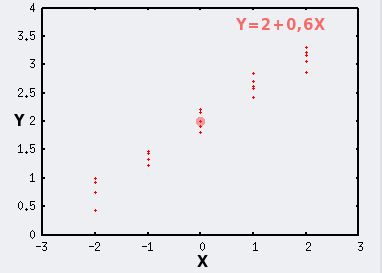
Lorsque la variable X est fixée, ici aux valeurs -2, -1, 0, 1 et 2, il n'y a plus de variabilité additionnelle sur X, et on visualise mieux la variabilité additionnelle qui ne concerne que Y, qui est toujours ici de paramètres μ=0 et σ=0,15. Le point de coordonnées (mX;mY) est symbolisé par le gros point rouge.
Le but de la régression est donc, face à une situation expérimentale, de chercher à quantifier ces sources de variabilités additionnelles verticales et horizontales, de manière à retrouver quel serait le modèle mathématique qui caractériserait au mieux la distribution des points si ces variabilités additionnelles, inévitables en conditions expérimentales, n'existaient pas.

Rappels :

Pour en savoir plus sur les modes de calculs de la pente et de l'ordonnée à l'origine :

• Si la variable X est aléatoire : module 20 : statistiques descriptives à deux dimensions
• Si la variable X est fixée : module 170 : la régression dans l'ANOVA1

Utilisons le même genre de démarche pour conceptualiser les fondements de la régression multiple, et détaillons les différents modes de régressions multiples linéaires.

Régression linéaire multiple à deux variables X

Prenons notre modèle de régression précédent (Y=2+0,6X) et rajoutons une variable aléatoire normale X₂.
Le modèle devient donc par exemple: Y=2+0,6X₁+1,2X₂

Rappel : Régression linéaire multiple à deux variables aléatoires: Modèle : Y=B0+B1X1+B2X2
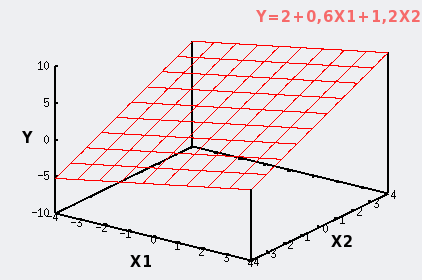
Le modèle idéal d'une régression linéaire multiple à deux variables X est un plan dans un espace à 3 dimensions (X1,X2,Y). Prenons un exemple ou Y=2+0,6X1+1,2X2. Ce modèle décrit la projection dans l'espace d'un plan défini par les deux droites d'équations : Y=2+0,6X1 dans le référentiel (X1,Y). Y=2+1,2X2 dans le référentiel (X2,Y).
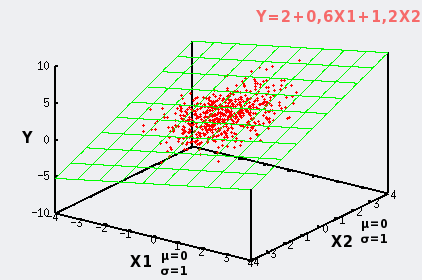
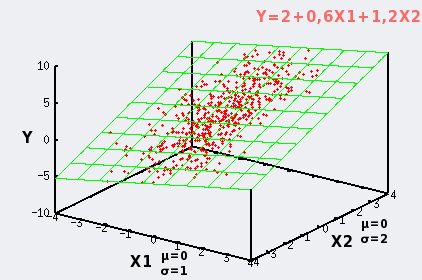
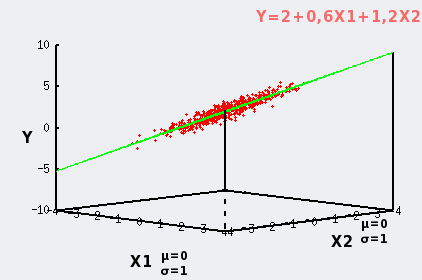
Lorsque X1 et X2 sont des variables aléatoires normales, les points se répartissent sur le plan selon l'intégration de deux distributions normales, et sont donc d'autant plus nombreux qu'on se rapproche du point dont les coordonnées sont (mX1;mX2;mY). La distribution des points sur le plan est donc influencée par les paramètres de distribution des X1 et X2, c'est-à-dire par une variabilité horizontale à deux dimensions. Dans notre premier exemple X1 et X2 sont des variables normales de paramètres μ=0 et σ=1. Dans ce cas le nuage de points est rond. Dans notre second exemple X1 et X2 n'ont pas le même écart-type σ: Dans ce cas le nuage de points est de forme ovale.
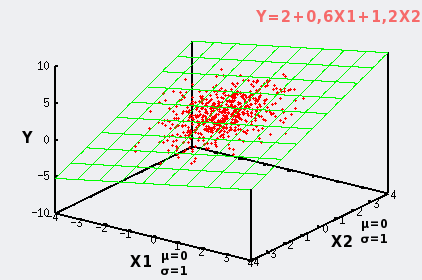
En conditions expérimentales, la distribution n'est jamais idéale. Des erreurs de mesures, des imprécisions, et des sources de variabilité d'origines diverses viennent s'ajouter au modèle normal. Dans ce cas les points ne se distribuent plus selon un plan parfait, mais selon un nuage, d'autant plus proche du plan parfait que ces variabilités supplémentaires sont faibles. Ces sources supplémentaires de variabilité, si X1, X2, et Y sont mesurés, influencent la distribution des points horizontalement si elles s'appliquent à X1 et X2, et verticalement si elles concernent Y. Dans notre exemple, pour simplifier les choses, nous avons résumé ces sources de variabilité supplémentaire en une variable aléatoire qui disperse les points verticalement par rapport au plan selon un modèle normal de paramètres μ=0 et σ=0,5. Pour bien conceptualiser ceci en 3D le même nuage de points est illustré sous deux perspectives différentes, la seconde étant dans l'axe du plan du modèle idéal: on voit alors que les points ne sont plus uniquement dans le plan, mais se répartissent de part et d'autres pour former un nuage en 3D.
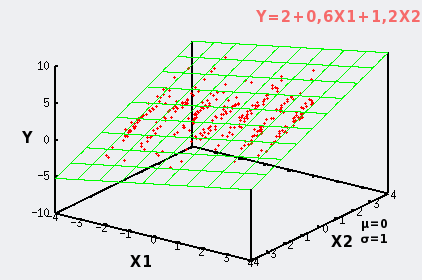
Lorsque la variable X1 est fixée, ici aux valeurs -3, -2, -1, 0, 1, 2, et 3, le nuage de points se résume à des tranches de variabilité. .
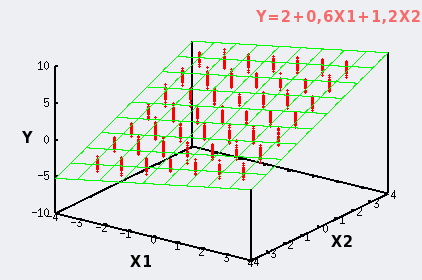
Lorsque les deux variables X1 et X2 sont de valeurs fixées, le nuage de points se résume à des colonnes de variabilité.
Le but de la régression est donc, face à une situation expérimentale, de chercher à quantifier ces sources de variabilités additionnelles verticales et horizontales, de manière à retrouver quel serait le modèle mathématique qui caractériserait au mieux la distribution des points si ces variabilités additionnelles, inévitables en conditions expérimentales, n'existaient pas.

Régression non-linéaire multiple à deux variables X

Dans la régression multiple le modèle est considéré comme non-linéaire à partir du moment où la distribution des points dans au moins une des dimensions ne suis pas un modèle linéaire

Exemples de régressions multiples non-linéaires
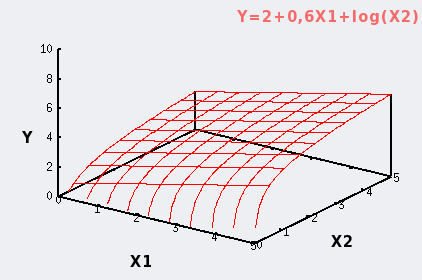
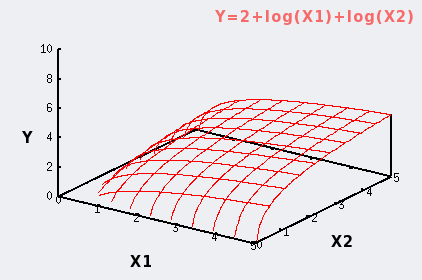
Les modèles non-linéaires étant fort nombreux nous nous contenterons ici de donner deux exemples de représentation graphique de cas de régression non-linéaire. Premier exemple : la relation entre Y et X1 suit un modèle linéaire, celle entre Y et X2 un modèle logarithmique. Y= 1+0,6X1 + log(X2). Deuxième exemple : les deux variables X ont une relation logarithmique avec Y. Y= 1+log(X1) + log(X2).

Le critère qui permet de déterminer le meilleur jeu de valeurs pour les paramètres B₀, B₁, B₂, B₃ … est la maximisation du coefficient de détermination

R² = Var(Y_modélisé)/ Var(Y_observé)

ou, ce qui revient au même, la minimisation globale des écarts entre les valeurs de Y modélisées et observées .

Le principe de la méthode consiste à développer l’équation de la somme des carrés des écarts entre les observations et le modèle, pour Y, (SCERy) et d’en calculer la dérivée partielle par rapport à chacun des paramètres. Le minimum de la fonction SCERy correspond au point où toutes les dérivées partielles sont nulles.

Ce système d’équation peut être résolu de façon analytique par le calcul matriciel suivant :

b = (X’X)^-1X’Y

X est une matrice de genre n x p comprenant l’ensemble des n valeurs de X₁, X₂ … X_p-1. On ajoute à X une colonne constante ( X_p=1 partout) pour estimer le paramètre libre B₀.

Y est un vecteur colonne n x 1 comprenant l’ensemble des n valeurs de Y

Le produit matriciel combine donc les genres suivants :

p x n ~ n x p ~ p x n ~ n x 1

Il est défini et produit le vecteur colonne b de genre p x 1, qui reprend la valeur des p paramètres B₀, B₁, B₂, … B_p-1.

La mortalité, la composition raciale (% de non blancs), un polluant atmosphérique (protoxyde d’azote, N₂O) et le niveau d’éducation ont été relevés dans quelques villes américaines (subset des données de http://lib.stat.cmu.edu/DASL/Datafiles/SMSA.html).

L’analyse à deux variables produit les résultats suivants :

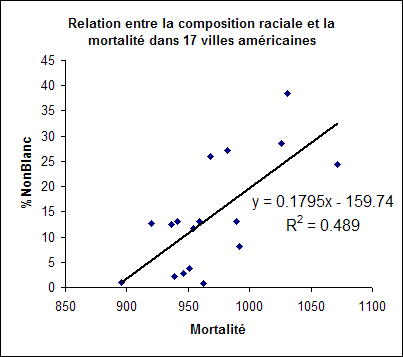
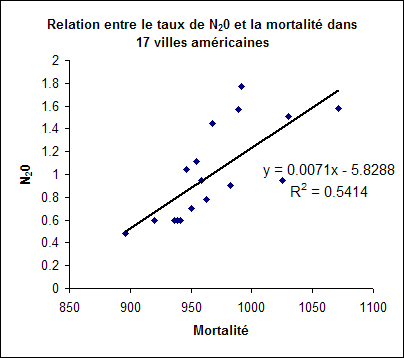
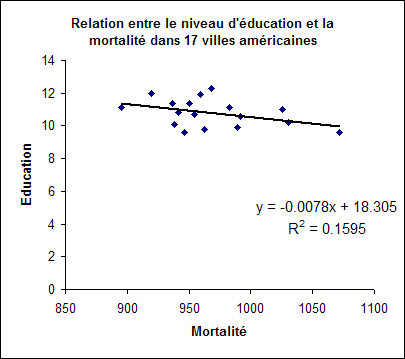
L’analyse en régression multiple se base sur les matrices suivantes :

Et produit le vecteur b calculé suivant:

b = (X’X)^-1X’Y

par la fonction excel :

=PRODUITMAT(INVERSEMAT(PRODUITMAT(TRANSPOSE(X);X));PRODUITMAT(TRANSPOSE(X);Y))

Les valeurs prédites par le modèle sont calculées  en appliquant l’équation:

Y_mod = 1109,57 + 36,04 X₁ + 2,29 X₂ -19,45 X₃

Soit une forte augmentation de la valeur prédictive pour la fonction des variables prises ensemble.

La question qui suit généralement l'approche par la régression multiple est de choisir parmi les variables X le plus petit nombre d'entre elles qui explique au mieux la variabilité de Y.

Une méthode courante est une régression itérative qui inclut d’abord dans le modèle la variable qui propose le meilleur coefficient de détermination. Ensuite, celle qui améliore le plus le coefficient de détermination et ainsi de suite.

Alternativement, toutes les variables sont entrées dans le modèle et les variables sont progressivement exclues, en fonction de celles qui contribuent le moins au modèle.

Il faut noter que la seconde variable qui entre dans le modèle n’est pas forcément celle qui présente, à elle seule, le second meilleur coefficient de détermination avec Y. Sinon, la solution serait triviale. En effet, X1 et X2 peuvent être très corrélées, voire quasi redondantes. Dans ce cas la qualité du modèle ne sera pas améliorée. C’est donc la variable qui contribue le plus à réduire la variabilité résiduelle, du modèle en voie d’élaboration qui sera sélectionnée à chaque étape.

La solution b = (X’X)^-1X’Y est mise en pratique par le logiciel Excel pour la régression linéaire simple et la régression polynomiale.

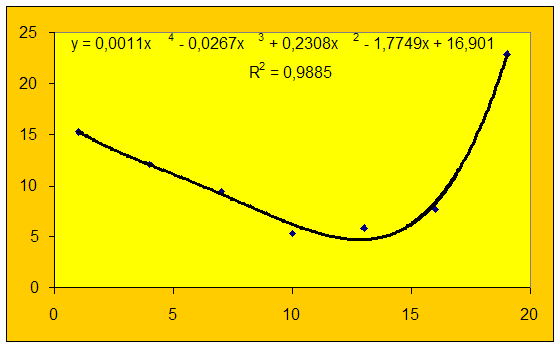
Exemple de régression polynomiale

(menu Graphique« Ajouter une courbe de tendance »)

Aucune solution n’est proposée pour le modèle linéaire multiple, mais le calcul se réalise facilement à l’aide des fonctions TRANSPOSE( ), PRODUITMAT( ) et INVERSEMAT( ).

Les modèles non-linéaires gérés par excel (logarithmique, exponentiel et puissance) sont calculés par la régression linéaire simple via la transformation de X et/ou de Y en log, la solution étant retransformée en anti-log.

Le logiciel Excel ne réalise pas de régression non linéaire proprement dite. Les fonctions sigmoïdes, multiples exponentielles, Michaëlis Menten … n’ont pas de solution analytique et doivent être réalisées par un logiciel qui propose un algorithme de minimisation numérique. A noter que même les fonctions linéarisables (exponentielle, puissance…) tirent avantage de cette approche.

Pour faire de l’inférence, notamment pour obtenir l’intervalle de confiance des paramètres, il est préférable d’utiliser un logiciel statistique plus sophistiqué que le tableur.

Les principes et les mises en garde concernant les limites de cette approche sont développés au module 20 dans le cadre de l’équation la plus simple Y = B0 + B1X1 . Ce sont les points spécifiques à la généralisation du modèle qui seront abordés ici.

Les précautions suivantes doivent être prises pour interpréter les résultats :

Plus on complexifie le modèle, plus la variabilité résiduelle peut être – apparemment- expliquée. Le nombre d’observations doit être relativement grand par rapport au nombre de variables incluses dans le modèle. Bien qu’il n’existe aucune règle absolue en cette matière on se référera au minimum à la règle empirique n > 2p

Les coefficients sont délicats à interpréter. En effet, B1 donne la variation de X1 correspondant à l’augmentation d’une unité de Y, pour autant que X2 reste constant. En pratique, cela est irréaliste car X1 est généralement corrélé à X2.

Les relations bivariées doivent préalablement être explorées graphiquement. La présence de données extrêmes ou aberrantes, la non linéarité de certaines relations, les écarts systématiques au modèle sont susceptibles d’affecter grandement les résultats.

Les conditions de linéarité étant souvent précaires et limitées à un domaine de X, l’extrapolation des résultats est toujours hasardeuse.

La régression polynomiale produit un modèle très « plastique » qui interpole bien les points mais ne possède aucune valeur d’extrapolation. La valeur des paramètres ne peut pas être associée à une explication structurelle du phénomène décrit.