Opérations d'une matrice par un scalaire ou un vecteur :
La matrice A peut subir toutes les opérations des scalaires (somme, différence, division, multiplication, exponentiation…). Cette opération s’effectue sur chacun de ses éléments.
Exemples:
Les opérateurs peuvent être rangés dans des vecteurs, pour autant que le nombre de lignes ou de colonnes soit adapté.
Opérations matricielles :
La plupart des opérations matricielles ne sont possibles qu’entre des matrices de genres adaptés à l’opération.
Exemple : Somme de matrices
La somme de deux matrices A et B implique que A et B soient toutes les deux de même genre n x p.
|
+ |
|
= |
|
|
|
|
|
|
A |
+ |
B |
= |
C |
{aij} |
+ |
{bij} |
= |
{cij} |
|
|
|
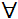 ij ij
|
|
Cas particulier: égalité de matrices
L’égalité de deux matrices A = B implique que aij= bij pour i, j, et donc n’est définie que si A et B sont toutes les deux de même genre n x p.
5 |
2 |
4 |
8 |
7 |
3 |
3 |
4 |
3 |
8 |
2 |
3 |
2 |
9 |
5 |
7 |
0 |
4 |
9 |
6 |
1 |
7 |
1 |
2 |
|
|
5 |
2 |
4 |
8 |
7 |
3 |
3 |
4 |
3 |
8 |
2 |
3 |
2 |
9 |
5 |
7 |
0 |
4 |
9 |
6 |
1 |
7 |
1 |
2 |
|
|
|
|
A |
= |
B |
{aij} |
= |
{bij} |
|
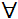 ij ij
|
|
|

