imprimer
Module 220:
Soit le prix d’un pain de 2 €. Ce prix est quantifié par un nombre réel a qualifié ici de nombre scalaire (sans direction), ce qui le différenciera des vecteurs, qui expriment une direction dans un espace.
a = 2 est un scalaire
Soit la liste de prix suivante (€):
1 pain |
2 |
1 kg jambon |
10 |
1 bac de bière |
12 |
1 bouteille d’eau |
1 |
1 vidange |
-0,1 |
La suite de nombres qui représente les prix constitue un vecteur, c’est-à-dire une collection de nombres d’une seule ligne ou d’une seule colonne.
|
2 |
|
|
10 |
|
a = |
12 |
est un vecteur colonne |
|
1 |
|
|
-0,1 |
|
a' = |
2 |
10 |
12 |
1 |
-0,1 |
est un vecteur ligne |
Transposition
La transposition est l’opération qui consiste à transformer le vecteur colonne a en vecteur ligne a’ et réciproquement : a’’ = a .
Notez qu’à ce stade le vecteur est une simple collection de nombres et que sa nature dirigée n’est pas prise en considération.
Soit la liste de courses suivante :
2 |
pains |
0,25 |
kg jambon |
1 |
bac de bière |
6 |
bouteilles d’eau |
10 |
Vidanges à rendre |
|
2 |
|
|
0,25 |
|
b = |
1 |
vecteur colonne |
|
6 |
|
|
10 |
|
b' = |
2 |
0,25 |
1 |
6 |
10 |
vecteur ligne |
Produit scalaire
Le produit scalaire est l’opération qui consiste à effectuer la somme des produits des éléments de deux vecteurs.
Exemple: produit scalaire b'a
Le produit scalaire b'a est la somme des produits des éléments de b’ par ceux de a.
Par définition, le vecteur situé à gauche est toujours un vecteur ligne et celui situé à droite est toujours un vecteur colonne.
Ceci implique que le nombre de colonnes de b’ doit être égal au nombre de lignes de a
|
Produit scalaire b'a : |
2 |
|
b'a=(2x2)+(10x0,25)+(12x1)
+(1x6)+(-0,1x10)=23,5 |
10 |
|
12 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
-0,1 |
|
2 |
0,25 |
1 |
6 |
10 |
23,5 |
|
Le scalaire obtenu représente le prix à payer à la caisse du magasin.
Le produit scalaire est transitif pour autant que les vecteurs soient transposés et leur ordre inversé:
b’a = a’b
|
Produit scalaire a'b : |
2 |
|
a'b=(2x2)+(0,25x10)+(1x12)
+(6x1)+(10x-0,1)=23,5 |
0,25 |
|
1 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
10 |
|
2 |
10 |
12 |
1 |
-0,1 |
23,5 |
|
Cas particulier: la forme quadratique a'a
La forme quadratique est le produit scalaire particulier a’a . Il correspond à la somme des carrés des éléments de a.
|
Forme quadratique a'a : |
2 |
|
a'b=(2²)+(10²)+(12²)+(1²)+(-0,1²)
=249,01 |
10 |
|
12 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
-0,1 |
|
2 |
10 |
12 |
1 |
-0,1 |
249,01 |
|
Une matrice A de genre n x p est une collection de p vecteurs colonnes aj de n lignes ou de n vecteurs lignes a’i de p colonnes. Tous les éléments aij doivent être définis : la matrice ne peut pas contenir de « trous ».
Soit la liste de prix suivante dans les trois magasins M1, M2, M3 :
|
M1 |
M2 |
M3 |
|
1 pain |
2 |
1,8 |
2,2 |
1 kg jambon |
10 |
8 |
15 |
1 bac de bière |
12 |
11 |
12 |
1 bouteille d’eau |
1 |
0,7 |
1,5 |
1 vidange |
-0,1 |
-0,1 |
-0,1 |
La matrice A de genre 5 x 3 reprend les prix de chaque article dans chaque magasin. La position de chaque élément aij est spécifique d’un article i et d’un magasin j.
| 2 |
1,8 |
2,2 |
| 10 |
8 |
15 |
| 12 |
11 |
12 |
| 1 |
0,7 |
1,5 |
| -0,1 |
-0,1 |
-0,1 |
Sur le plan informatique, on peut considérer la matrice B de genre 6 x 4 qui reprend également l’intitulé des articles et des magasins.
| |
M1 |
M2 |
M3 |
| 1 pain |
2 |
1,8 |
2,2 |
| 1 kg jambon |
10 |
8 |
15 |
| 1 bac de bière |
12 |
11 |
12 |
| 1 bouteille d'eau |
1 |
0,7 |
1,5 |
| 1 vidange |
-0,1 |
-0,1 |
-0,1 |
Dans ce genre de matrice, on peut imaginer que certains éléments aij soient manquants. Si M3 ne vend pas de pain, l’élément a24 comprendra un code tel que "n.d." (non disponible ou non défini).
| |
M1 |
M2 |
M3 |
| 1 pain |
2 |
1,8 |
n.d. |
| 1 kg jambon |
10 |
8 |
15 |
| 1 bac de bière |
12 |
11 |
12 |
| 1 bouteille d'eau |
1 |
0,7 |
1,5 |
| 1 vidange |
-0,1 |
-0,1 |
-0,1 |
Toutefois cet exposé se limite à des matrices réelles (tous les aij sont des nombres réels).
Important:
La validité des calculs suppose que la valeur 0 signifie réellement une valeur réelle nulle et ne signifie pas : donnée non disponible.
Opérations d'une matrice par un scalaire ou un vecteur :
La matrice A peut subir toutes les opérations des scalaires (somme, différence, division, multiplication, exponentiation…). Cette opération s’effectue sur chacun de ses éléments.
Exemples:
Les opérateurs peuvent être rangés dans des vecteurs, pour autant que le nombre de lignes ou de colonnes soit adapté.
Opérations matricielles :
La plupart des opérations matricielles ne sont possibles qu’entre des matrices de genres adaptés à l’opération.
Exemple : Somme de matrices
La somme de deux matrices A et B implique que A et B soient toutes les deux de même genre n x p.
|
+ |
|
= |
|
|
|
|
|
|
A |
+ |
B |
= |
C |
{aij} |
+ |
{bij} |
= |
{cij} |
|
|
|
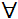 ij ij
|
|
Cas particulier: égalité de matrices
L’égalité de deux matrices A = B implique que aij= bij pour i, j, et donc n’est définie que si A et B sont toutes les deux de même genre n x p.
5 |
2 |
4 |
8 |
7 |
3 |
3 |
4 |
3 |
8 |
2 |
3 |
2 |
9 |
5 |
7 |
0 |
4 |
9 |
6 |
1 |
7 |
1 |
2 |
|
|
5 |
2 |
4 |
8 |
7 |
3 |
3 |
4 |
3 |
8 |
2 |
3 |
2 |
9 |
5 |
7 |
0 |
4 |
9 |
6 |
1 |
7 |
1 |
2 |
|
|
|
|
A |
= |
B |
{aij} |
= |
{bij} |
|
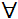 ij ij
|
|
La matrice A de genre n x p peut être transposée en matrice A’ de genre p x n en transposant la collection des p vecteurs colonnes aj de n lignes en p vecteurs lignes a’i de n colonnes.
Exemple:
Une matrice A de 6 lignes sur 4 colonnes devient une matrice A' de 4 lignes sur 6 colonnes.
| 5 |
2 |
4 |
8 |
| 7 |
3 |
3 |
4 |
| 3 |
8 |
2 |
3 |
| 2 |
9 |
5 |
7 |
| 0 |
4 |
9 |
6 |
| 1 |
7 |
1 |
2 |
|
|
| 5 |
7 |
3 |
2 |
0 |
1 |
| 2 |
3 |
8 |
9 |
4 |
7 |
| 4 |
3 |
2 |
5 |
9 |
1 |
| 8 |
4 |
3 |
7 |
6 |
2 |
|
|
|
|
A = {aij} |
|
A' = {a'ji} |
Cas particuliers : matrices carrées et matrices symétriques
Une matrice carrée est une matrice où les nombres de lignes et de colonnes sont égaux. Leur genre est alors n x n ou p x p. Une matrice est dite symétrique dans le cas particulier où elle est identique à sa transposée: A = A’ (ce qui implique que A est forcément carrée).
| 5 |
7 |
3 |
2 |
| 7 |
3 |
8 |
9 |
| 3 |
8 |
2 |
5 |
| 2 |
9 |
5 |
7 |
|
= |
| 5 |
7 |
3 |
2 |
| 7 |
3 |
8 |
9 |
| 3 |
8 |
2 |
5 |
| 2 |
9 |
5 |
7 |
|
| |
|
|
A = {aij} |
= |
A' = {aji} |
| |
|
|
Notez qu’une diagonale particulière apparaît en {aii}. Elle contient les seules valeurs de la matrice symétrique qui ne sont pas dupliquées. Les valeurs {aij} pour tous les i≠j se « reflètent en miroir » de part et d’autre de cette diagonale.
| 5 |
7 |
3 |
2 |
| 7 |
3 |
8 |
9 |
| 3 |
8 |
2 |
5 |
| 2 |
9 |
5 |
7 |
Le produit matriciel AB est la généralisation du produit scalaire entre les lignes de A et les colonnes de B.
Imaginons qu’une association de consommateurs teste le prix de 4 listes d’achats dans 3 magasins M1, M2, M3.
Client |
1 |
2 |
3 |
4 |
|
pains |
2 |
0 |
10 |
0 |
kg jambon |
0,3 |
3 |
0 |
6 |
bac de bière |
1 |
2 |
5 |
0 |
bouteille d’eau |
6 |
16 |
0 |
24 |
Vidanges à rendre |
0 |
0 |
0 |
0 |
Prix (€) |
M1 |
M2 |
M3 |
|
1 pain |
2 |
1,8 |
2,2 |
1 kg jambon |
10 |
15 |
8 |
1 bac de bière |
12 |
11 |
12 |
1 bouteille d’eau |
1 |
1,5 |
0,8 |
1 vidange |
-0,1 |
-0,1 |
-0,1 |
Soit A la matrice des quantités de genre 5 x 4 et B 5 x3 la matrice des prix unitaires.
| 2 |
0 |
10 |
0 |
| 0,3 |
3 |
0 |
6 |
| 1 |
2 |
5 |
0 |
| 6 |
16 |
0 |
24 |
| 0 |
0 |
0 |
0 |
|
|
| 2 |
1,8 |
2,2 |
| 10 |
15 |
8 |
| 12 |
11 |
12 |
| 1 |
1,5 |
0,8 |
| -0,1 |
-0,1 |
-0,1 |
|
| |
|
|
A |
|
B |
Le prix à payer par chaque client dans chaque magasin est donné par le produit A’B = C
A’ : 4 x 5, B : 5 x 3, C : 4 x 3
| |
| 2 |
1,8 |
2,2 |
| 10 |
15 |
8 |
| 12 |
11 |
12 |
| 1 |
1,5 |
0,8 |
| -0,1 |
-0,1 |
-0,1 |
|
B |
|
| |
M1 |
M2 |
M3 |
| Client 1: |
25 |
28,1 |
23,6 |
| Client 2: |
70 |
91 |
60,8 |
| Client 3: |
80 |
73 |
82 |
| Client 4: |
84 |
126 |
67,2 |
|
|
| 2 |
0,3 |
1 |
6 |
0 |
| 0 |
3 |
2 |
16 |
0 |
| 10 |
0 |
5 |
0 |
0 |
| 0 |
6 |
0 |
24 |
0 |
|
| 25 |
28,1 |
23,6 |
| 70 |
91 |
60,8 |
| 80 |
73 |
82 |
| 84 |
126 |
67,2 |
|
C=A'B |
-> |
|
A' |
|
|
|
|
|
La liste d’articles dans la liste d’achat doit forcément correspondre élément par élément à la liste d’articles dans la liste de prix : le nombre de colonnes de A doit être égal au nombre de lignes de B.
La faisabilité d’un produit matriciel et le genre de la matrice produite se lit aisément en représentant les genres par un jeu de dominos :
A’ : 4 x 5 |
B : 5 x 3 |
|
 |
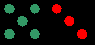 |
les extrémités en contact correspondent:
le produit A'B est possible et la matrice produite aura pour genre les valeurs extérieures. |
|
C : 4 x 3 |
|
| |
|
|
B : 5 x 3 |
A’ : 4 x 5 |
|
 |
 |
les extrémités en contact ne correspondent pas :
le produit BA' est impossible. |
Le produit matriciel n’est donc pas commutatif: A'B ≠ BA'. Par la contrainte du genre des partenaires, il ne pourrait l’être qu’entre matrices carrées, mais ce n’est pas le cas, sauf particularité.
Par contre la transposée du produit AB peut s’écrire B'A'= (AB)'
Exemple: B'A=(A'B)'
| |
| 2 |
0 |
10 |
0 |
| 0,3 |
3 |
0 |
6 |
| 1 |
2 |
5 |
0 |
| 6 |
16 |
0 |
24 |
| 0 |
0 |
0 |
0 |
|
A |
|
|
|
| 2 |
10 |
12 |
1 |
-0,1 |
| 1,8 |
15 |
11 |
1,5 |
-0,1 |
| 2,2 |
8 |
12 |
0,8 |
-0,1 |
|
| 25 |
70 |
80 |
84 |
| 28,1 |
91 |
73 |
126 |
| 23,6 |
60,8 |
82 |
67,2 |
|
B'A |
est la transposée de |
A'B |
| 25 |
28,1 |
23,6 |
| 70 |
91 |
60,8 |
| 80 |
73 |
82 |
| 84 |
126 |
67,2 |
|
B' |
|
|
|
|
Exemple interactif de produit matriciel :
Les deux matrices à fond blanc sont interactives: vous pouvez changer les valeurs dans les cellules, et visualiser le résultat directement dans la matrice à fond gris.
NB: pour valider un changement de valeur: "enter" dans firefox, "tab" dans safari et internet-explorer. Utiliser le point comme symbole décimal
La matrice identité I est une matrice symétrique dont la diagonale principale est remplie de 1 et les autres éléments de 0. Elle joue dans le produit matriciel le même rôle que l’unité dans le produit entre scalaires :
5 x 1 = 1 x 5 = 5
AI = IA = A
| |
| 2 |
9 |
0 |
4 |
3 |
| 8 |
2 |
4 |
0 |
5 |
| 0 |
9 |
9 |
9 |
1 |
| 0 |
5 |
9 |
3 |
8 |
|
A |
| 1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
|
| 2 |
9 |
0 |
4 |
3 |
| 8 |
2 |
4 |
0 |
5 |
| 0 |
9 |
9 |
9 |
1 |
| 0 |
5 |
9 |
3 |
8 |
|
A=I.A |
I |
|
|
| |
|
|
| |
| 1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
1 |
|
I |
| 2 |
9 |
0 |
4 |
3 |
| 8 |
2 |
4 |
0 |
5 |
| 0 |
9 |
9 |
9 |
1 |
| 0 |
5 |
9 |
3 |
8 |
|
| 2 |
9 |
0 |
4 |
3 |
| 8 |
2 |
4 |
0 |
5 |
| 0 |
9 |
9 |
9 |
1 |
| 0 |
5 |
9 |
3 |
8 |
|
A=A.I |
A |
|
|
Il est convenu que la matrice I a le genre qu’il faut pour que le produit soit défini. On constatera dans l’expression ci-dessus que la matrice I à droite de A n’est pas identique à la matrice I à gauche de A, sauf si A est carrée. La notation ne les distingue cependant pas.
Exemple interactif de produit par la matrice identité :
Les deux matrices à fond blanc sont interactives: Vous pouvez changer les valeurs dans les cellules, et visualiser le résultat directement dans la matrice à fond gris.
NB: pour valider un changement de valeur: "enter" dans firefox, "tab" dans safari et internet-explorer. Utiliser le point comme symbole décimal
La matrice inverse de A, matrice carrée, est notée A-1 et joue dans le produit matriciel le même rôle que l’unité dans l’inverse entre scalaires :
5 x 1/5 = 1/5 x 5 = 1
A-1A = AA-1= I
|
|
A-1 |
| |
A |
| 0,2 |
-0,8 |
-0,4 |
0,2 |
| -0,3 |
0 |
0,5 |
0 |
| 0,1 |
0,2 |
0,1 |
0 |
| 0,1 |
0,2 |
-0,2 |
0 |
|
A-1 |
| 2 |
0 |
10 |
0 |
| 0,3 |
3 |
0 |
6 |
| 1 |
2 |
5 |
0 |
| 6 |
16 |
0 |
24 |
|
| 1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
|
| 0,2 |
-0,8 |
-0,4 |
0,2 |
| -0,3 |
0 |
0,5 |
0 |
| 0,1 |
0,2 |
0,1 |
0 |
| 0,1 |
0,2 |
-0,2 |
0 |
|
| 1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
|
I |
|
|
|
Certaines matrices, dites singulières, ne peuvent pas s’inverser. C'est le cas des matrices dont une ligne ou colonne est une combinaison linéaire d’une autre.
Il existe une matrice A+ inverse généralisée, ou pseudo-inverse, de A non carrée et/ou singulière telle que :
A+A A+ = A bien que A+A ≠ A A+ ≠ I
Le calcul de la matrice inverse généralisée est lié à la diagonalisation de la matrice, vue dans le module consacré aux valeurs propres.
Norme et angles
Examinons le produit A’A de la matrice A constituée des 3 vecteurs colonnes représentés en rouge, bleu et vert:
| |
|
A |
|
| 10 |
2,83 |
0 |
| 2,83 |
1 |
2,83 |
| 0 |
2,83 |
40 |
|
A'A |
A' |
|
|
Tableau 8: 1 Coordonnées, norme et produit scalaire
de 3 vecteurs (représentation graphique ci-dessous)
La diagonale de la matrice correspond à la forme quadratique de chaque vecteur. En appliquant le théorème de Pythagore, la somme des carrés des coordonnées du vecteur correspond au carré de sa longueur (norme du vecteur). Noter le vecteur bleu de norme et de longueur égales à l’unité.
Le produit scalaire entre les vecteurs est lié au cosinus de l’angle formé par leur représentation géométrique sur la figure ci-dessous. Le seul qui nous intéresse ici est le produit scalaire nul entre les vecteurs rouge et vert, qui forment un angle droit.

Figure 8 : 1 Représentation géométrique des vecteurs de la table ci-dessus
matrice orthogonale :
Une matrice orthogonale C est une matrice carrée telle que C-1 = C’
Cette matrice nous intéresse dans la mesure où elle est capable d’effectuer une rotation orthogonale d’un jeu de vecteurs dans un espace.
Considérons le produit matriciel suivant :
Le produit donnant une matrice I , C’ est bien l’inverse de C.
Considérons à présent que les valeurs de C correspondent à la matrice
Cos(45°) |
Sin(45°) |
-Sin(45°) |
Cos(45°) |
Et regardons le résultat du produit CA , puis (CA)’(CA) :
| |
|
| 1,00 |
0,71 |
6,00 |
| 3,00 |
0,71 |
-2,00 |
|
A |
| C |
|
| 2,83 |
1,00 |
2,83 |
| 1,41 |
0,00 |
-5,66 |
|
CA |
| |
| 2,83 |
1,41 |
| 1,00 |
0,00 |
| 2,83 |
-5,66 |
|
| 10 |
2,83 |
0 |
| 2,83 |
1 |
2,83 |
| 0 |
2,83 |
40 |
|
(CA)'(CA) |
Constatons que le produit (CA)’(CA) est IDENTIQUE au produit A’A ci-dessus. La longueur des vecteurs et les angles qu’ils forment entre eux sont IDENTIQUES.
Constatons sur le graphique la rotation de 45° du jeu de vecteurs :

Figure 8-2: Le produit de A par la matrice orthogonale C a donc effectué une rotation de 45° en préservant sans aucune distorsion de l’espace.
La rotation orthogonale joue un rôle essentiel en analyse mutlivariée.
Vous êtes invités à télécharger le fichier Excel pour généraliser cette constatation à différents angles.
 ij
ij