Supposons que l'on réalise une expérience portant sur l'étude de la pression sanguine (Y variable aléatoire) en fonction de l'âge (X variable contrôlée):
Lorsque l'âge des patients augmente, va-t-on observer un accroissement de leur pression sanguine?
Cet accroissement répond-il à un modèle linéaire?
| Age |
20 |
30 |
40 |
50 |
60 |
70 |
| valeurs |
120 |
123 |
134 |
130 |
142 |
145 |
125 |
120 |
128 |
137 |
136 |
138 |
121 |
126 |
127 |
135 |
139 |
141 |
118 |
125 |
131 |
133 |
141 |
148 |
Ce que nous savons déjà:
Une simple analyse descriptive nous a permis les conclusions suivantes:
-
Le coefficient de corrélation r vaut environ 0,94. L'interprétation à donner est la suivante: "Si la relation entre X et Y est de type linéaire, elle est croissante, car le r est positif. De plus, comme le r est très proche de 1, on peut supposer que le nuage de points est très concentré autour de la droite de régression. Il est cependant impossible de tirer une conclusion ferme et définitive sur la linéarité de la relation tant que le graphique n'a pas été réalisé (méthode empirique), ou qu'un test sur la linéarité de la relation n'a pas été effectué (méthode statistique)."
-
Le coefficient de détermination R2 vaut environ 0,88. L'interprétation à donner est la suivante: "Si la relation entre X et Y est de type linéaire, le modèle mathématique Y=aX+b peut expliquer à lui seul 88% de la variabilité observée. Les 12% restants représentent les erreurs de mesures et toutes les imprécisions engendrées lors de l'expérience. Comme au point précédent, sans la visualisation graphique de l'expérience, ou un test statistique sur la linéarité, il est impossible d'affirmer avec certitude que la relation est bien linéaire."
-
Grâce à la représentation graphique (diagramme de dispersion), nous pouvons confirmer que le modèle linéaire semble bien adapté à la répartition des points car il est possible de faire passer une droite par le nuage des points, mais rien ne nous prouve que c'est ce modèle qui explique au mieux la distribution des points.
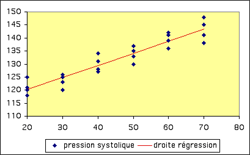
Pression systolique (Y aléatoire) en fonction de l'âge du patient (X fixe)
Une analyse de ce type reste assez simpliste et il n'est pas possible de savoir à coup sûr si la relation est bien linéaire! Pour cela il faut réaliser un test statistique sur la linéarité de la distribution, test que nous allons détailler à la page suivante.
|

