Une expérience fait parfois intervenir une série statistique à deux dimensions, c'est-à-dire 2 séries d'observations X et Y couplées. Lorsqu'au moins une des 2 variables est aléatoire, il est possible de considérer ces 2 variables simultanément au moyen d'une régression.

2 variables aléatoires	X = abondance d'une récolte (variable aléatoire)
	Y = nombre de jours d'ensoleillement (variable aléatoire)
1 variable aléatoire et une variable contrôlée	X = température fixée (variable contrôlée)
	Y = nombre de graines germées (variable aléatoire)

Cas étudié dans le cadre de ce cours:

Dans le cadre de ce cours, seul le cas où X est une variable contrôlée (non aléatoire, c'est-à-dire de valeurs fixées par l'expérimentateur) sera considéré.

Conditions d'utilisation de la régression dans l'ANOVA :

Condition 1:

Les valeurs prises par la variable X doivent être fixées sans erreur par l'expérimentateur.

Condition 2

X étant une variable contrôlée, on peut considérer Y comme fonction de X, mais pas le contraire :

Y=f(X)

Condition 3:

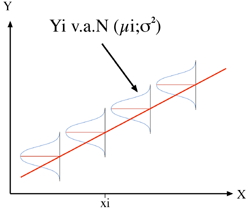
Pour chaque valeur X_i de X, il existe une population de valeurs Y_i distribuée normalement, de moyenne µ_i et de variance σ² homogène c'est-à-dire constante quelle que soit la valeur de X :

Y_i v.a.N(µ_i; σ²)

Condition 4:

Les moyennes µ_i correspondant aux valeurs Y_i sont situées sur une droite dont les paramètres sont ß0 et ß1 telle que :

µ_i=ß0+ß1X_i

avec ß0 l'ordonnée à l'origine et ß1 la pente

Condition 5:

Les variables aléatoires Y_i sont indépendantes.