Illustrons les trois sommes des carrés des écarts intervenant dans l'ANOVA sur base d'un exemple d'une expérience regroupant 18 vaches réparties en 3 échantillons de 6 individus.

SCET : Somme des carrés des écarts totaux

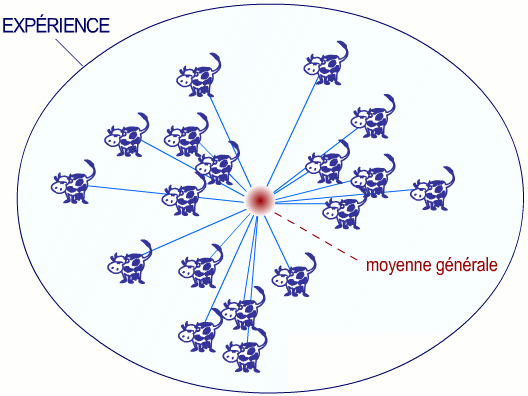
Elle reflète les écarts existant entre chaque individu de l'expérience et la moyenne générale, peu importe l'échantillon auquel les individus appartiennent.
Elle représente la variabilité totale au sein de l'expérience.

Degrés de libertés : N-1 (N=nombre total d'individus dans l'expérience.)
Dans notre exemple dl_SCET=18-1=17

Calcul dans Excel ou OpenOffice:
=SOMME.CARRES.ECARTS(série des données).

SCEF : Somme des carrés des écarts factoriels

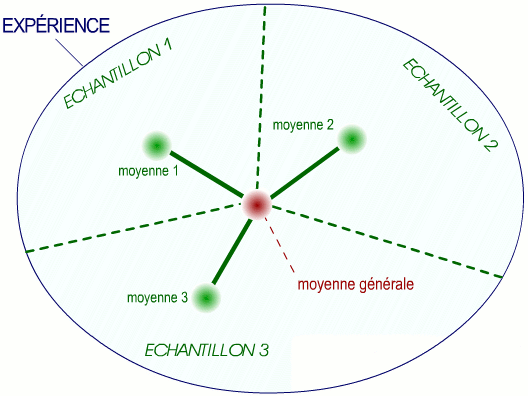
Elle reflète les écarts existant entre les moyennes de chaque échantillon et celle de l'expérience.
Elle représente la variabilité due aux différences entre échantillons, et donc la variabilité due à l'existence d'un facteur de variation.

Degrés de libertés : na-1 (na=nombre d'échantillons dans l'expérience.)
Dans notre exemple dl_SCEF=3-1=2

Calcul dans Excel ou OpenOffice:
=ni*SOMME.CARRES.ECARTS(série des moyennes des échantillons)
avec ni = nombre d'individus par échantillon.

SCER : Somme des carrés des écarts résiduels

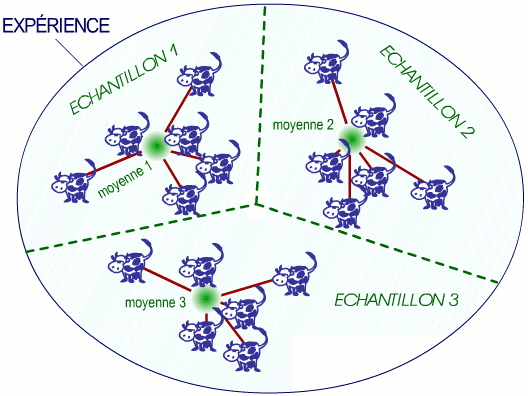
Elle reflète les écarts existant entre chaque individu et la moyenne de son propre échantillon.
Elle représente la variabilité existant au sein des échantillons, c'est-à-dire celle qui ne peut être expliquée par la présence du facteur de variation.

Degrés de libertés : N-na
Dans notre exemple dl_SCER=18-3=15

Calcul dans Excel ou OpenOffice:
=(ni-1)*SOMME(série des variances des échantillons).