Ce test s'applique lorsqu'on possède une hypothèse qui prédit les fréquences, les pourcentages ou les proportions. Le but est de vérifier si les fréquences observées s'accordent avec les prévisions du modèle.

En règle générale, les données se représentent sous la forme d'un tableau de distribution de fréquences composé de k colonnes (ex: k échantillons à comparer) comparées à r lignes (r catégories ou classes inventoriées par échantillon).

Exemple et pose des hypothèses:

Le gène codant pour la couleur des yeux comprend plusieurs variants (allèles). Chaque allèle donne une couleur d'yeux bien déterminée. Les proportions des deux allèles sont de 75% de dominants (allèle yeux bruns) pour 25% de récessifs (allèle yeux bleus).

Hypothèse initiale (hypothèse nulle H0): L'allèle "yeux bruns" est dominant par rapport à l'allèle "yeux bleus". Les proportions suivent un modèle 25% "yeux bleus" contre 75% "yeux bruns".

Hypothèse alternative (H1): Le modèle de proportions 25% "yeux bleus" contre 75% "yeux bruns" n'est pas valable.

Méthode:

Un expérimentateur choisit 100 individus au hasard dans une population et trouve 32 individus aux yeux bleus contre 68 aux yeux bruns. Il dresse le tableau suivant et calcule les fréquences théoriques sur base de la taille de l'échantillon mis à sa disposition et des proportions décrites par le modèle H0:

	yeux bruns	yeux bleus	Total
fréquences observées	68	32	100
fréquences théoriques	75	25	100

Le calcul de chi-carré observé s'effectue en employant la formule:

= (fréquence observée - fréquence théorique) ² / fréquence théorique

comme suit:

	yeux bruns	yeux bleus	Total
Chi carrés observés	(68-75)2/75 =0,653333333	(32-25)2/25 =1,96	2,613333333

Il faut comparer cette valeur observée à une valeur de chi-carré théorique de référence (un seuil de signification) dans des tables de référence. Cette table est une table à double entrée:

• L'entrée en ligne nécessite de connaître les degrés de liberté de l'expérience. Il se calcule de la manière suivante: (k-1) avec k le nombre de colonnes (dans le test de conformité il n'y a qu'une ligne). Dans un cas simple comme celui présenté ici où il existe plusieurs classes (colonnes) mais une seule ligne, les degrés de liberté à employer sont (k-1).
• L'entrée en colonne est déterminée par l'expérimentateur. C'est en effet lui qui détermine la confiance du test.

Dans l'exemple, il n'y a qu'une ligne pour deux colonnes, soit 1 degré de liberté. Supposons que l'on prenne un intervalle de confiance à 95% (alpha 5%), la valeur de chi-carré des tables est:

1dl;0,95= 3,84

Le test est unilatéral à droite puisque le calcul du chi-carré observé génère uniquement des valeurs positives.

Si le chi-carré observé est plus grand que le chi-carré théorique, alors on rejette l'hypothèse nulle (RH0). Dans ce cas, on considère que le modèle 25% "yeux bleus" contre 75% "yeux bruns" (H0) n'est pas valide.

Conclusion de l'exemple:

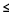
observé [=2,61333] 1dl;0,95[=3,84]

Le modèle décrit dans l'hypothèse nulle (H0) est plausible. On accepte H0. Jusqu'à preuve du contraire, la population obéit bien à une répartition 25% (allèle "yeux bleus") contre 75% (allèle "yeux bruns").