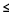imprimer
Module 135:
Rappel:
La loi du  est une loi dérivée de la loi normale. Très importante
pour ses applications en statistiques, elle est utilisée pour
tester des statistiques basées sur le calcul de la somme des
carrés des écarts.
est une loi dérivée de la loi normale. Très importante
pour ses applications en statistiques, elle est utilisée pour
tester des statistiques basées sur le calcul de la somme des
carrés des écarts.
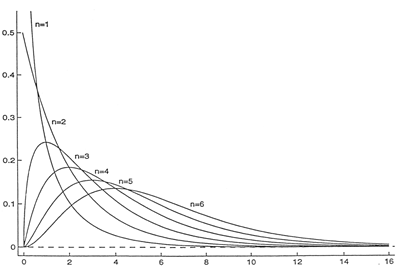
A partir de
3 degrés de liberté, les distributions  suivent une distribution en cloche caractérisée par une
dissymétrie à gauche. La forme de la courbe est déterminée
par le nombre de degrés de liberté. Le nombre de degrés
de liberté dépend du nombre de catégories dans
lesquelles les fréquences sont dénombrées. En effet,
plus le nombre de degrés de liberté augmente, plus
suivent une distribution en cloche caractérisée par une
dissymétrie à gauche. La forme de la courbe est déterminée
par le nombre de degrés de liberté. Le nombre de degrés
de liberté dépend du nombre de catégories dans
lesquelles les fréquences sont dénombrées. En effet,
plus le nombre de degrés de liberté augmente, plus  tend vers une v.a. Normale et donc adopte une courbe en cloche.
tend vers une v.a. Normale et donc adopte une courbe en cloche.
Types de tests :
Dans le cadre de ce cours de statistiques élémentaires,
nous ne nous préoccuperons que de deux types de tests différents:
- le test d'indépendance
- le test de conformité d'un
échantillon à un standard
Ce test s'applique lorsqu'on souhaite démontrer l'indépendance ou la dépendance de deux critères dans une expérience portant sur une v.a. discrète.
Soit plusieurs échantillons pouvant être classés selon un certain nombre de colonnes (critère 1) et de lignes (critère 2).
Exemple et pose des hypothèses:
Supposons la situation suivante: Au cours d'une enquête, on interroge 1 369 mères d'enfants nés avec au moins une malformation et 2 968 mères d'enfants nés sans malformation.
On constate que 35,06% des mères d'enfants nés avec au moins une malformation et 33,02% des mères d'enfants nés sans malformation fumaient.
Effectuez l'analyse statistique complète de ces résultats.
Hypothèse initiale (hypothèse nulle H0): le fait d'avoir au moins une malformation à la naissance ne dépend pas du fait que la mère soit fumeuse ou non. Les deux critères sont indépendants.
Hypothèse alternative (H1): Les 2 critères "avoir un enfant avec au moins une malformation ou non " et "être issu une mère fumeuse ou non" sont dépendants (liés)
Remarque: Dans cet exemple, "être un enfant avec au moins une malformation ou normal" constitue 2 états du critère 1 et "être issu d'une mère non fumeuse ou fumeuse" constitue 2 états du critère 2. Il faut cependant noter que le nombre d'états de chaque critère n'est pas restreint à 2.
Méthode:
Grâce aux données fournies par l'énoncé, il est possible de réaliser le tableau suivant:
| valeurs observées: |
enfant avec au moins une malformation |
enfant sans malformation |
Total |
mère fumeuse |
480 |
980 |
1460 |
mère non fumeuse |
889 |
1988 |
2877 |
| Total |
1369 |
2968 |
4337 |
Dans ce tableau, on retrouve les fréquences expérimentales mais aussi les totaux par lignes (1460 enfants sont nés de mères fumeuses contre 2877 de mères non fumeuses) et par colonnes (1369 enfants sont nés avec au moins une malformation contre 2968 enfants normaux) ainsi que le nombre total d'individus analysés dans l'expérience (4337).
En suivant le modèle H0 , il est possible d'estimer des valeurs théoriques sur base des valeurs expérimentales. La manière d'y parvenir est décrite dans le tableau suivant:
valeurs théoriques: |
enfant avec au moins une malformation |
enfant sans malformation |
|
mère fumeuse |
= 1369 *1460 / 4337 = 460,85 |
= 2968 *1460 / 4337 = 999,15 |
1460 |
mère non fumeuse |
= 1369 * 2877 / 4337 = 908,14 |
= 2968 * 2877 / 4337 = 1968,86 |
2877 |
|
1369 |
2968 |
4337 |
Pour mesurer, sur l'ensemble des catégories, la différence entre les fréquences observées et théoriques, on réduit les écarts suivant la méthode du  :
:
 = (fréquence observée - fréquence théorique)2 / fréquence théorique = (fréquence observée - fréquence théorique)2 / fréquence théorique |
On obtient alors le tableau suivant:
|
enfant avec au moins une malformation |
enfant sans malformation |
|
mère fumeuse |
(480 - 460,85)2 / 460,85 |
(980 - 999,15)2 / 999,15 |
|
mère non fumeuse |
(889 - 908,14)2 / 908,14 |
(1988 - 1968,86)2 / 1968,86 |
|
|
|
|
|
ou encore:
|
enfant avec au moins une malformation |
enfant sans malformation |
mère fumeuse |
0,783 |
0,361 |
mère non fumeuse |
0,397 |
0,183 |
Pour tirer une conclusion sur la dépendance (H1) ou l'indépendance (H0), on somme tous les  observés:
observés:
 = 0,783 + 0,361 + 0,397 + 0,183 = 1,72
= 0,783 + 0,361 + 0,397 + 0,183 = 1,72
Et on compare ensuite cette valeur globale à une valeur des tables
Cette table est une table à double entrée:
- L'entrée en ligne nécessite de connaître le nombre de degrés de liberté de l'expérience. Il se calcule de la manière suivante: (k-1).(r-1) avec k le nombre de colonnes et r le nombre de lignes.
- L'entrée en colonne est déterminée par l'expérimentateur. C'est en effet lui qui détermine la confiance du test.
Conclusion de l'exemple:
Dans l'exemple, il n'y a que 2 lignes pour deux colonnes, soit (2-1)*(2-1) degrés de liberté. Supposons que l'on prenne un intervalle de confiance à 95% (alpha 5%), la valeur de chi-carré des tables est:
 1dl;0,95= 3,84
1dl;0,95= 3,84
 Le test est unilatéral à droite puisque le calcul du chi-carré observé génère uniquement des valeurs positives.
Le test est unilatéral à droite puisque le calcul du chi-carré observé génère uniquement des valeurs positives.
Si le chi-carré observé est plus grand que le chi-carré théorique au seuil alpha, alors on rejette l'hypothèse nulle (RH0).
Dans ce cas, on a un  observé de 1,72. Cette valeur est inférieure à 3,84 (la valeur des tables). On accepte H0. Cela implique que les mères fumeuses n'ont pas plus ou moins de chance de donner naissance à un enfant avec au moins une malformation qu'une mère non fumeuse. Les deux critères sont indépendants, je n'ai pas réussi à le montrer.
observé de 1,72. Cette valeur est inférieure à 3,84 (la valeur des tables). On accepte H0. Cela implique que les mères fumeuses n'ont pas plus ou moins de chance de donner naissance à un enfant avec au moins une malformation qu'une mère non fumeuse. Les deux critères sont indépendants, je n'ai pas réussi à le montrer.
Ce test s'applique lorsqu'on possède une hypothèse qui
prédit les fréquences, les pourcentages ou les proportions.
Le but est de vérifier si les fréquences observées
s'accordent avec les prévisions du modèle.
En règle générale, les données se représentent
sous la forme d'un tableau de distribution de fréquences composé
de k colonnes (ex: k échantillons à comparer) comparées
à r lignes (r catégories ou classes inventoriées par
échantillon).
Exemple et pose des hypothèses:
Le gène codant pour la couleur des yeux comprend plusieurs variants
(allèles). Chaque allèle donne une couleur d'yeux bien déterminée.
Les proportions des deux allèles sont de 75% de dominants (allèle
yeux bruns) pour 25% de récessifs (allèle yeux bleus).
Hypothèse initiale (hypothèse
nulle H0): L'allèle "yeux bruns" est
dominant par rapport à l'allèle "yeux
bleus". Les proportions suivent un modèle
25% "yeux bleus" contre 75% "yeux bruns".
Hypothèse
alternative (H1): Le modèle de proportions 25%
"yeux bleus" contre 75% "yeux bruns"
n'est pas valable.
Méthode:
Un expérimentateur choisit
100 individus au hasard dans une population et trouve 32 individus aux
yeux bleus contre 68 aux yeux bruns. Il dresse le tableau suivant et calcule
les fréquences théoriques sur base de la taille de l'échantillon
mis à sa disposition et des proportions décrites par le modèle
H0:
| |
yeux bruns |
yeux bleus |
Total |
| fréquences observées |
68 |
32 |
100 |
| fréquences théoriques |
75 |
25 |
100 |
Le calcul de chi-carré observé s'effectue en employant
la formule:
 =
(fréquence observée - fréquence théorique)
2 / fréquence théorique
=
(fréquence observée - fréquence théorique)
2 / fréquence théorique
comme suit:
| |
yeux bruns |
yeux bleus |
Total |
| Chi carrés observés |
(68-75)2/75
=0,653333333 |
(32-25)2/25
=1,96 |
2,613333333 |
Il faut comparer cette valeur observée à une valeur de
chi-carré théorique de référence (un seuil
de signification) dans des tables de référence. Cette table
est une table à double entrée:
- L'entrée en ligne nécessite
de connaître les degrés de liberté de l'expérience.
Il se calcule de la manière suivante: (k-1) avec k le
nombre de colonnes (dans le test de conformité il n'y a qu'une
ligne). Dans un cas simple comme celui présenté ici où
il existe plusieurs classes (colonnes) mais une seule ligne, les degrés
de liberté à employer sont (k-1).
- L'entrée en colonne est déterminée par
l'expérimentateur. C'est en effet lui qui détermine la
confiance du test.
Dans l'exemple, il n'y a qu'une ligne pour deux colonnes, soit 1 degré
de liberté. Supposons que l'on prenne un intervalle de confiance
à 95% (alpha 5%), la valeur de chi-carré des tables est:
 1dl;0,95= 3,84
1dl;0,95= 3,84
 Le
test est unilatéral à droite puisque le calcul
du chi-carré observé génère
uniquement des valeurs positives.
Le
test est unilatéral à droite puisque le calcul
du chi-carré observé génère
uniquement des valeurs positives.
Si le chi-carré observé
est plus grand que le chi-carré théorique, alors on rejette
l'hypothèse nulle (RH0). Dans ce cas, on considère que le
modèle 25% "yeux bleus" contre 75% "yeux bruns"
(H0) n'est pas valide.
Conclusion de l'exemple:
 observé [=2,61333]
observé [=2,61333] 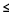
 1dl;0,95[=3,84]
1dl;0,95[=3,84]
Le modèle décrit dans
l'hypothèse nulle (H0) est plausible. On accepte H0. Jusqu'à
preuve du contraire, la population obéit bien à une répartition
25% (allèle "yeux bleus") contre 75% (allèle
"yeux bruns").
1. Au cours d'une étude cas-témoin réalisée
dans un hôpital, 317 patientes souffrant d'un cancer de l'endomètre
ont été appariées à 317 patientes saines. La
prise d'œstrogènes durant les 6 mois précédant
le diagnostic a été déterminée. On a observé
que 54 femmes saines et 152 femmes qui ont développé le
cancer avaient pris des œstrogènes.
Faites l'analyse de ces proportions.
2. Au cours d'un essai clinique, 184 personnes ont reçu le médicament
traditionnel et 103 personnes ont reçu un nouveau médicament.
Avec le médicament traditionnel, on a observé 129 guérisons
et avec le nouveau 80. Faites l'analyse des proportions.
3. 2 000 personnes sont suivies pendant 20 ans, 800 sont fumeurs et 1200
non fumeurs. Au cours des 20 ans de suivi, on observe 100 cas de cancer:
90 chez les fumeurs, 10 chez les non fumeurs.
Effectuez l'analyse statistique.
4. Voici les fréquences des différents types de cultures
selon le type de sol. Faites l'analyse de ce tableau:
| |
cultures de prairies |
vignes et vergers |
bois et broussailles |
| plaine |
167 |
124 |
42 |
| versant |
10 |
30 |
80 |
| sommet |
11 |
0 |
16 |
5. Lors d'une étude sur la pollution
bactérienne, la présence ou l'absence de salmonelles
a été recensée à partir d'échantillons
d'eau prélevés dans 3 bassins européens.
Les analyses fournissent les résultats suivants :
| |
Rhin |
Loire |
Seine |
| Présence de salmonelles |
8 |
10 |
16 |
| Absence de salmonelles |
2 |
11 |
23 |
Peut-on affirmer que la Seine est moins polluée
que le Rhin et la Loire?
[source: http://www.obs-vlfr.fr/~enseigne/maitp6/solution_test/testexo16.htm]
6. Un vétérinaire recense 4 cas de brucellose dans un
gros élevage extensif de moutons du Larzac comptant 1230 têtes.
Ce résultat invalide-t-il de façon significative le modèle
épidémiologique affirmant que la maladie ne touche en principe
qu'un individu sur 1000?
7. On a effectué le croisement de balsamines blanches avec des
balsamines pourpres. En première génération, les
fleurs sont toutes pourpres. On obtient en deuxième génération
quatre catégories avec les effectifs suivants:
| Couleur |
pourpre |
rose |
blanc-lavande |
blanc |
| Effectifs |
1790 |
547 |
548 |
213 |
Peut-on accepter l'hypothèse de répartition mendélienne
(9/16; 3/16; 3/16; 1/16)?
8. En général, on enregistre 15 naissances gémellaires
sur 1000 naissances. En Suède, une étude a été
menée sur 30000 femmes enceintes et 840 femmes ont donné
naissance à des jumeaux. Peut-on considérer que la Suède
est significativement "hors normes"?
![]() est une loi dérivée de la loi normale. Très importante
pour ses applications en statistiques, elle est utilisée pour
tester des statistiques basées sur le calcul de la somme des
carrés des écarts.
est une loi dérivée de la loi normale. Très importante
pour ses applications en statistiques, elle est utilisée pour
tester des statistiques basées sur le calcul de la somme des
carrés des écarts.
![]() suivent une distribution en cloche caractérisée par une
dissymétrie à gauche. La forme de la courbe est déterminée
par le nombre de degrés de liberté. Le nombre de degrés
de liberté dépend du nombre de catégories dans
lesquelles les fréquences sont dénombrées. En effet,
plus le nombre de degrés de liberté augmente, plus
suivent une distribution en cloche caractérisée par une
dissymétrie à gauche. La forme de la courbe est déterminée
par le nombre de degrés de liberté. Le nombre de degrés
de liberté dépend du nombre de catégories dans
lesquelles les fréquences sont dénombrées. En effet,
plus le nombre de degrés de liberté augmente, plus ![]() tend vers une v.a. Normale et donc adopte une courbe en cloche.
tend vers une v.a. Normale et donc adopte une courbe en cloche.