1. Concentration en LH:

Test de conformité d'une moyenne (test de Z Unidirectionnel)

H0: µ1 = µ0

H1: µ1 < µ0

z_observé = -2,77

Pour α=5%, Z_tables = -1,64, donc on conclut RH0 car z_observé inférieur à Z_tables

Pour α=1% Z_tables = -2,33, donc on conclut RH0 car z_observé inférieur à Z_tables

Conclusion: La prise du contraceptif X provoque une diminution hautement significative de la concentration en LH. L'ovulation ne peut avoir lieu. [retour aux énoncés]

2. Fécondité en France et en Belgique:

Homogénéité des variances:

H0: σ²₁ = σ²₂

H1: σ²₁ ≠ σ²₂

F_obs= (427,68/99) / (281,24/79) = 1,21

F_{0,975; 99dl; 79dl} = 1,53

F_obs < F_{0,975; 99dl; 79dl} donc il y a AH0 -> On n'a pas pu montrer que les variances étaient différentes. Le test d'hypothèses portant sur les moyennes est donc réalisable.

Test d'hypothèses:

Comparaison de 2 moyennes tirées d'échantillons indépendants (test de t unidirectionnel à gauche si nous prenons les femmes belges comme référence)

H0: µB = µF

H1: µB > µF

S_r²_obs=( 427,68+281,24)/(100+80-2) = 3,98

t_obs = (1,78-2,12)/(3,98*(1/100+1/80))^0,5= -1,136 NDLR: X^0,5= racine de x

t_{0,05; 178dl} = -1,653

t_obs supérieur à t_{0,05; 178dl} donc conclusion: AH0, nous n'avons pas pu montrer que les femmes françaises étaient moins fécondes que les femmes belges

[retour aux énoncés]

3. Les boulons:

Test unidirectionnel à droite (par exemple) avec une valeur critique

µ + valeur des tables*ET/(n)^0,5

Rendre l'intervalle de confiance 5 fois plus petit signifie que la valeur critique devient:

µ + valeur des tables*ET/(n)^0,5 * (1/5)

ou encore:

µ + valeur des tables*ET/(25*n)^0,5

et donc, l'échantillon doit être 25 fois plus grand. Soit 2500 pièces pour être sûr de voir une augmentation de l'écart à la normalité.

[retour aux énoncés]

4. Consommation en Irlande et en Angleterre:

Sur base de l'énoncé on peut postuler : µ₀ = 1%; µ₁=1,5%; S²=1,9%²

La consultation de la dernière ligne de la table de Student nous donne les valeurs de z suivantes :
Z_1-alpha = Z_0,95 = 1,645
Z_1-beta = Z_0,99 = 2,326

En appliquant la formule disponible dans votre formulaire :

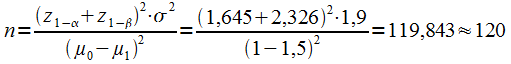
En prenant 120 ménages dans les deux pays étudiés, nous pourrons voir cette différence de dépenses.[retour aux énoncés]

5. Les raisins:

Test de comparaison de 2 moyennes tirées de 2 populations indépendantes.

1°) Test de l’homogénéité des variances

H0: σ²₁=σ²₂

H1: σ²₁ différent de σ²₂

F_observé = 0.011/0.007 = 1.57

F_{tables (6 dl; 10 dl; 0.975)} = 4.07

F_observé inférieur à F_tables donc on conclut AH0 (je n’ai pas pu montrer l'hétérogénéité des variances)

2°) Comparaison des moyennes:

H0: µ1 = µ2

H1: µ1 différent de µ2

t_observé = 1.77

avec S_r²_observé = 0.0085

t_{tables (16 dl; 0.975)} = 2.12

t_observé inférieur à t_tables donc on conclut AH0 pour α=5%.

[retour aux énoncés]

6. Un procédé de fabrication de tubes T.V.

Test de conformité d'une moyenne (test de Z Unidirectionnel)

H0: µ1=µ0

H1: µ1 supérieur à µ0

Z_observé= 2.17

5% Z_tables = 1.64 RH0 car Z_observé supérieur à Z_tables

Conclusion: Le nouveau procédé de fabrication possède une durée de vie significativement plus importante que l’ancien procédé.

[retour aux énoncés]

7. Un enseignant et ses groupes d’étudiants:

Test de comparaison de 2 moyennes tirées de 2 populations indépendantes.

A. Entre A et B:

1°) Test de l’homogénéité des variances

H0: σ²_A = σ²_B

H1: σ²_A différent de σ²_B

F_observé = 4.69

F_{tables (16 dl; 16 dl; 0.975)} = 2.76

F_observé supérieur à F_tables donc on conclut RH0 (les variances ne sont pas identiques)

Impossible de comparer les moyennes tirées d’échantillons dont les variances sont hétérogènes.

B. Entre A et C:

1°) Test de l’homogénéité des variances

H0: σ²_A = σ²_C

H1: σ² différent de σ²_C

F_observé = 1.16

F_{tables (16 dl; 16 dl; 0.975)} = 2.76

F_observé inférieur à F_tables donc on conclut AH0 (les variances sont homogènes)

2°) Comparaison des moyennes:

H0: µA = µC

H1: µA supérieur à µC

t_observé = 2.39

avec S²_observé = 16.0998

t_{tables (32 dl; 0.95)} = 1.697

t_{tables (32 dl; 0.99)} = 2.457

Le groupe A possède une moyenne significativement plus grande que la moyenne du groupe C. Ce test n’est pas hautement significatif.

C. Entre B et C:

1°) Test de l’homogénéité des variances

H0: σ²_B = σ²_C

H1: σ²_B différent de σ²_C

F_observé = 4.04

F_{tables (16 dl; 16 dl; 0.975)} = 2.76

F_observé supérieur à F_tables donc on conclut RH0 (les variances ne sont pas identiques)

Impossible de comparer les moyennes tirées d’échantillons dont les variances sont hétérogènes.

[retour aux énoncés]

8. Analyse des triglycérides:

Test de comparaison entre deux échantillons tirés de populations pairées (les mêmes patients, les mêmes prélèvements MAIS des méthodes différentes).

H0: µA = µB

H1: µA différent de µB

t_observé = 3.26

t_{tables (9dl; 0.975)} = 2.262

t_{tables (9dl; 0.995)} = 3.25

Les 2 méthodes d’analyses des triglycérides donnent des résultats très différents (différence très significative).

[retour aux énoncés]

9. Techniques de mesure de température sur un troupeau de 30 vaches:

Test de comparaison entre deux échantillons tirés de populations pairées (les mêmes vaches, les mêmes températures MAIS des techniques différentes).

H0: µ_mercure = µ_infra-rouge

H1: µ_mercure différent de µ_infra-rouge

t_observé = 1.99

t_{tables (29 dl; 0.975)} = 2.045

Nous n'avons pas pu montrer que les 2 techniques d’analyses de la température donnaient des résultats différents.

[retour aux énoncés]

10. Influence du cadmium sur le taux de glucose dans le sang chez la truite:

Nous pouvons donc réaliser un test de comparaison de 2 moyennes tirées de 2 populations indépendantes et rechercher un Z observé (car les variances des populations avec et sans Cd sont connues et valent respectivement 5 et 10 (mg de glucose/l)² ).

H0: m_{sans Cd} = m_{avec Cd}

H1: m_{sans Cd} supérieur à m_{avec Cd}

Z_observé = 5,039

z_{(tables 0.95)} = 1.645

z_{(tables 0.99)} = 2.326

Le Cd augmente la glycémie de manière hautement significative (RH0 à alpha = 1%)

[retour aux énoncés]