1. Comparaison de dépenses en soins de santé entre deux pays
Des études de consommation ont été réalisées
en Irlande et en Angleterre. Les dépenses en services médicaux
et dépenses de santé représentaient, en 1985, respectivement
1,5% et 1% de la consommation totale des ménages. Sachant qu'en Europe,
la variation des dépenses en services médicaux et dépenses
de santé est de 1,9 (%²), combien de ménages doit-on
étudier (alpha = 5%) dans ces deux pays pour montrer, dans 99% des
cas, que la consommation totale en Irlande est supérieure à
celle obtenue en Angleterre?
Correction :
Sur base de l'énoncé on peux postuler : µ0 = 1%; µ1=1,5%; σ²=1,9%²
La consultation de la dernière ligne de la table de Student nous donne les valeurs de z suivantes :
Z1-α = Z0,95 = 1,645
Z1-β = Z0,99 = 2,326
En appliquant la formule disposnible dans votre formulaire :
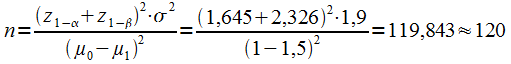
En prenant 120 ménages dans les deux pays étudiés, nous pourrons voir cette différence de dépenses.
2. Etude d'un médicament hypertenseur
Soit une expérience portant sur l'étude d'un médicament
hypertenseur expérimental. L'expérience est menée sur
des rats de laboratoire dont on connait la pression sanguine habituelle:
(120±15) mm de mercure.
L'effet attendu doit être plus grand que 124 mm de mercure (effet
obtenu avec un médicament commercialisé depuis des années
et bien caractérisé).
Questions :
a ) De combien d'individus a-t-on besoin pour voir un effet dans 99% des cas
sachant que l'intervalle de confiance est de 95%?
b ) Qu'en est-il avec une population de rats homogènes (même âge et même sexe) pour laquelle la variance est de 25mm²?
Correction :
a ) De combien d'individus a-t-on besoin pour voir un effet dans 99% des cas
sachant que l'intervalle de confiance est de 95%?
Sur base de l'énoncé on peux postuler : µ0 = 124 mm ; µ1=120 mm ; σ²=225 mm²
La consultation de la dernière ligne de la table de Student nous donne les valeurs de z suivantes :
Z1-α = Z0,95 = 1,645
Z1-β = Z0,99 = 2,326
En reprenant la même formule qu'à l'exercice 1 : ((1,645+2,326)²x225)/((124-120)²) = 221,7 ≈ 222 donc n ≥ 222
b ) Qu'en est-il avec une population de rats homogènes (même âge et même sexe) pour laquelle la variance est de 25mm²?
Sur base de l'énoncé on peux postuler : µ0 = 124 mm ; µ1=120 mm ; σ²=25 mm²
La consultation de la dernière ligne de la table de Student nous donne les valeurs de z suivantes :
Z1-α = Z0,95 = 1,645
Z1-β = Z0,99 = 2,326
En reprenant la même formule qu'à l'exercice 1 : ((1,645+2,326)²x25)/((124-120)²) = 24,67 ≈ 25 donc n ≥ 25

