Module 120:

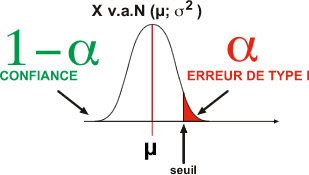
Lors d'un test d'hypothèses, l'expérimentateur tente de montrer que la moyenne de l'échantillon n'est pas conforme à la population qui lui sert de référence. Pour réaliser son test, il doit donc décomposer arbitrairement la courbe de Gauss représentant la population de référence en 2 parties distinctes:

Si le modèle Ho est correct (modèle Ho)

1. alpha (ou erreur de type I): la probabilité de considérer la moyenne observée comme non conforme
2. 1-alpha (ou confiance): la probabilité de considérer la moyenne observée comme conforme

Si la moyenne observée est comprise dans la zone alpha, l'expérimentateur peut tirer une conclusion:

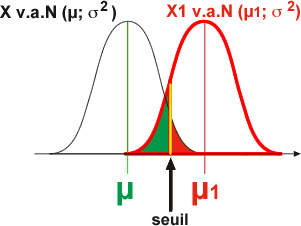
2. Voir un effet qui existe:

Si la moyenne observée est comprise dans la zone alpha, cela peut signifier aussi que l'échantillon d'où provient la valeur observée est constitué d'individus appartenant à une population de moyenne (µ1) distincte de µ (en rouge: cas où il existe une population centrée sur une moyenne µ1 plus grande que µ).

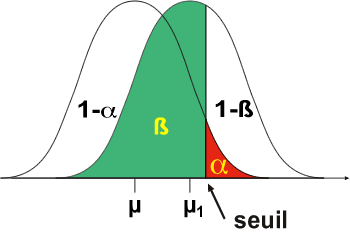
Le modèle H1 est représenté ici à droite du modèle Ho.

Dans le cas présent: H1 (µ1 supérieur à µ), représente un accroissement hypothétique du paramètre étudié, déplaçant ainsi la courbe à droite. Attention, il y a une différence fondamentale entre le modèle Ho, qui est centré sur une moyenne m connue et le modèle H1, centré sur une moyenne m inconnue.

Ce modèle H1 est donc représenté à un endroit tout à fait arbitraire.

Le seuil de signification définit sous la courbe deux zones distinctes:

une zone où l'expérimentateur ne voit pas un effet qui existe réellement: c'est l'ERREUR DE TYPE II, représentée par ß. une zone où l'expérimentateur voit un effet qui existe réellement: c'est la PUISSANCE, représentée par (1-ß).

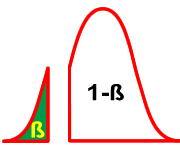
L'objectif de l'expérimentateur sera de mettre toutes les chances de son côté afin de voir le plus souvent possible un effet si cet effet existe réellement. Il va devoir jouer sur certains paramètres pour diminuer le recouvrement des deux courbes.

Non optimisé:
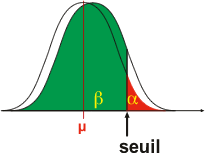alpha: 5% confiance: 95%
bêta: 85% puissance:15%
En d'autres termes, l'expérimentateur devra augmenter la puissance (1-ß) le plus possible (par exemple 99%) et donc diminuer la probabilité de ne pas mettre en évidence un effet qui existe réellement (l'erreur de type II ß) à environ 1% SANS MODIFIER LA CONFIANCE du test.
Optimisé:
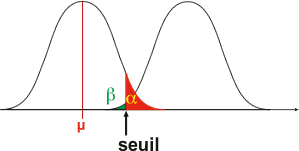alpha: 5% confiance: 95%
bêta: 1% puissance: 99%

Animation :

animation en pleine page

Supposons qu'un laboratoire pharmaceutique demande à l'un de ses chercheurs de montrer qu'une molécule X provoque une augmentation de la pression sanguine chez le rat.

L'employé doit mettre toutes les chances de son côté pour démontrer cet accroissement de la pression sanguine, pour cela, il peut contrôler les paramètres suivants s'ils existent :

	PARAMETRE	COMMENT LE MODIFIER ?	EFFET	MODIFIABLE?
1	µ1	Augmenter la dose du médicament	Augmentation de la distance entre les modèles
2	Variance de la population	Cibler au mieux la population (rats mâles de 3 mois non stressés)	Resserrement des courbes autour de leur moyenne
3	Taille d'échantillon	Augmenter la taille de l'échantillon	Resserrement des courbes autour de leur moyenne
4	alpha	Augmenter alpha	Augmentation de RH0 même si pas d'effet à observer

En augmentant la dose du médicament X jusqu'à une concentration n'entraînant pas trop de décès chez les rats, l'expérimentateur peut contraindre la courbe "avec effet" à se déplacer vers la droite.

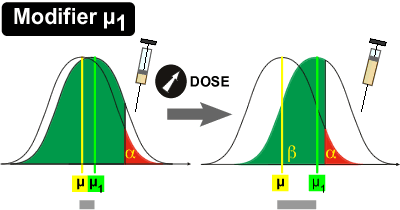
La moyenne µ1 s'éloigne de plus en plus de la moyenne µ de référence jusqu'à une valeur optimale (si la dose de médicament est plus importante, elle provoque la mort des rats).

Il en résulte une diminution de la superposition des deux courbes et donc une augmentation de la puissance.

exemple: µ = 120 mm de mercure; µ1 avant optimisation de la dose = 122 mm de Hg; µ1 après optimisation de la dose = 124 mm de Hg

Comment optimiser une expérience pour voir un effet le plus souvent possible?

2. Modifier la variabilité de la population étudiée:

Dans notre exemple, un expérimentateur novice risque de prendre n'importe quel rat provenant de l'animalerie de son laboratoire. Il risque de prendre des rats dont les caractéristiques sont très différentes.

La population des rats de laboratoire comporte des rats mâles et femelles, des jeunes et des vieux, des stressés et des non stressés. Tous ces facteurs entraînent une augmentation significative de la variabilité.

En ciblant la population (par exemple: la population des rats mâles de 3 mois non stressés) on va diminuer sa variabilité. L'implication graphique de cette diminution de la variabilité se traduit par un resserrement de la courbe de Gauss autour de la moyenne.

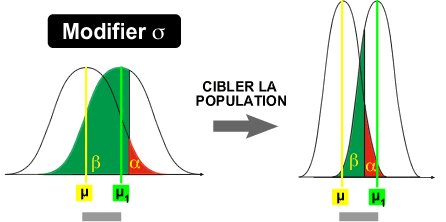
Il en résulte une diminution de la superposition des deux courbes et donc une augmentation de la puissance.

exemple: variance pour tous les rats = 225 [mm de Hg]2; variance pour des rats mâles de 3 mois non stressés = 25 [mm de Hg]2

Comment optimiser une expérience pour voir un effet le plus souvent possible?

3. Modifier la taille de l'échantillon:

La modification de la taille de l'échantillon a un effet similaire à celui observé lorsque l'expérimentateur réduit la variabilité de la population.

Le théorème de la limite centrale nous apprend que la distribution d'échantillonnage des moyennes obéit à une distribution normale centrée sur µ et dont la variance est VARx/n.

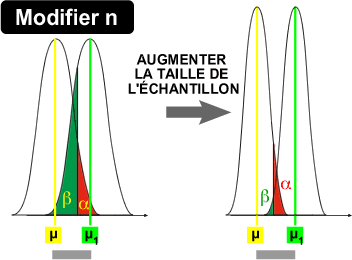
Pour ne pas devoir augmenter de manière exagérée la taille de l'échantillon à traiter, il est recommandé d'optimiser préalablement la distance entre µ et µ1 (augmenter la dose) et de réduire au maximum la variabilité de la population étudiée AVANT d'augmenter la taille de l'échantillon.

Supposons le test d'hypothèses suivant:

• H0: µ = µ1 = 120
• H1: µ1 supérieur à µ = 120
• Confiance 95%

NB: L'expérimentateur peut déterminer la taille optimale de son échantillon pour avoir une puissance donnée à condition de fixer µ-µ1 minimal.

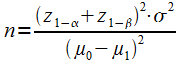
Comment optimiser une expérience pour voir un effet le plus souvent possible?

4. Augmenter alpha:

Un expérimentateur doit diminuer au maximum le recouvrement entre le modèle Ho et H1.

Il serait tenté d'augmenter la surface alpha afin d'accroître la puissance (1-ß). Cette pratique n'est cependant pas recommandée.

L'expérimentateur délimite arbitrairement un intervalle de confiance (1-alpha) et une erreur de type I (alpha) mais par définition alpha doit être petit.

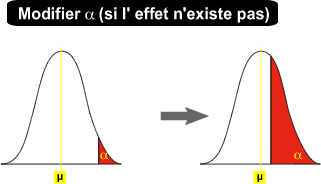
En augmentant alpha, l'expérimentateur rejettera plus souvent l'hypothèse nulle à tort.

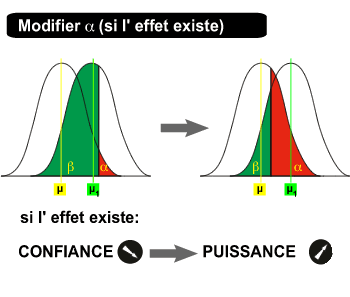
Si on réalise un test avec un grand alpha :

• En cas de RHo, la confiance est faible.
• En cas d'AHo, le risque d'erreur est inconnu.

Aucune décision n'est fiable.

En conclusion:

Si la valeur observée se retrouve dans la zone de rejet de l'hypothèse nulle, cela veut dire que:

1. elle appartient à la population de référence mais, par hasard, il a obtenu une valeur observée qui est très éloignée de la moyenne de la population de référence. La probabilité de l'obtenir dans cette population de référence est très faible mais pas impossible.
2. elle est trop éloignée de la moyenne de la population de référence. Elle n'a pas été obtenue par hasard et, par conséquent, le modèle H1 est très vraisemblable.

Remarques:

1. Comparaison de dépenses en soins de santé entre deux pays

Des études de consommation ont été réalisées en Irlande et en Angleterre. Les dépenses en services médicaux et dépenses de santé représentaient, en 1985, respectivement 1,5% et 1% de la consommation totale des ménages. Sachant qu'en Europe, la variation des dépenses en services médicaux et dépenses de santé est de 1,9 (%²), combien de ménages doit-on étudier (alpha = 5%) dans ces deux pays pour montrer, dans 99% des cas, que la consommation totale en Irlande est supérieure à celle obtenue en Angleterre?

Correction :

Sur base de l'énoncé on peux postuler : µ₀ = 1%; µ₁=1,5%; σ²=1,9%²

La consultation de la dernière ligne de la table de Student nous donne les valeurs de z suivantes :
Z_1-α = Z_0,95 = 1,645
Z_1-β = Z_0,99 = 2,326

En appliquant la formule disposnible dans votre formulaire :

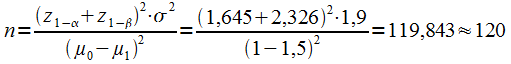
En prenant 120 ménages dans les deux pays étudiés, nous pourrons voir cette différence de dépenses.

2. Etude d'un médicament hypertenseur

Soit une expérience portant sur l'étude d'un médicament hypertenseur expérimental. L'expérience est menée sur des rats de laboratoire dont on connait la pression sanguine habituelle: (120±15) mm de mercure.

L'effet attendu doit être plus grand que 124 mm de mercure (effet obtenu avec un médicament commercialisé depuis des années et bien caractérisé).

Questions :

a ) De combien d'individus a-t-on besoin pour voir un effet dans 99% des cas sachant que l'intervalle de confiance est de 95%?

b ) Qu'en est-il avec une population de rats homogènes (même âge et même sexe) pour laquelle la variance est de 25mm²?

Correction :

a ) De combien d'individus a-t-on besoin pour voir un effet dans 99% des cas sachant que l'intervalle de confiance est de 95%?

Sur base de l'énoncé on peux postuler : µ₀ = 124 mm ; µ₁=120 mm ; σ²=225 mm²

La consultation de la dernière ligne de la table de Student nous donne les valeurs de z suivantes :
Z_1-α = Z_0,95 = 1,645
Z_1-β = Z_0,99 = 2,326

En reprenant la même formule qu'à l'exercice 1 : ((1,645+2,326)²x225)/((124-120)²) = 221,7 ≈ 222 donc n ≥ 222

b ) Qu'en est-il avec une population de rats homogènes (même âge et même sexe) pour laquelle la variance est de 25mm²?

Sur base de l'énoncé on peux postuler : µ₀ = 124 mm ; µ₁=120 mm ; σ²=25 mm²

La consultation de la dernière ligne de la table de Student nous donne les valeurs de z suivantes :
Z_1-α = Z_0,95 = 1,645
Z_1-β = Z_0,99 = 2,326

En reprenant la même formule qu'à l'exercice 1 : ((1,645+2,326)²x25)/((124-120)²) = 24,67 ≈ 25 donc n ≥ 25