Comment optimiser une expérience pour voir un effet le plus souvent possible?

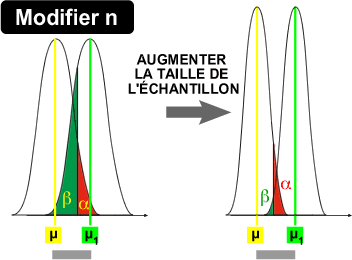
3. Modifier la taille de l'échantillon:

La modification de la taille de l'échantillon a un effet similaire à celui observé lorsque l'expérimentateur réduit la variabilité de la population.

Le théorème de la limite centrale nous apprend que la distribution d'échantillonnage des moyennes obéit à une distribution normale centrée sur µ et dont la variance est VARx/n.

Pour ne pas devoir augmenter de manière exagérée la taille de l'échantillon à traiter, il est recommandé d'optimiser préalablement la distance entre µ et µ1 (augmenter la dose) et de réduire au maximum la variabilité de la population étudiée AVANT d'augmenter la taille de l'échantillon.

Supposons le test d'hypothèses suivant:

• H0: µ = µ1 = 120
• H1: µ1 supérieur à µ = 120
• Confiance 95%

CAS	Paramètres	taille minimale de n pour une puissance de 99% et une confiance de 95%
1	µ1=122 VARx =225	887 rats
2	µ1=124 VARx =225	222 rats
3	µ1=122 VARx =25	99 rats
4	µ1=124 VARx =25	25 rats

NB: L'expérimentateur peut déterminer la taille optimale de son échantillon pour avoir une puissance donnée à condition de fixer µ-µ1 minimal.

µ1 reste inconnu, mais la différence µ-µ1 peut être inintéressante en dessous d'un certain seuil.
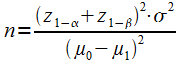