Lors d'un test d'hypothèses, l'expérimentateur tente de montrer que la moyenne de l'échantillon n'est pas conforme à la population qui lui sert de référence. Pour réaliser son test, il doit donc décomposer arbitrairement la courbe de Gauss représentant la population de référence en 2 parties distinctes:

Si le modèle Ho est correct (modèle Ho)

1. alpha (ou erreur de type I): la probabilité de considérer la moyenne observée comme non conforme
2. 1-alpha (ou confiance): la probabilité de considérer la moyenne observée comme conforme

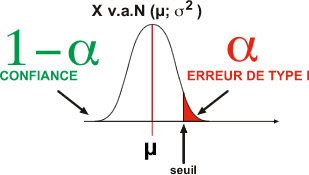
Si la moyenne observée est comprise dans la zone alpha, l'expérimentateur peut tirer une conclusion:

1. Voir un effet qui n'existe pas:

TOUS LES INDIVIDUS SOUS CETTE COURBE SONT CONFORMES

Si la moyenne observée est comprise dans la zone alpha, cela peut signifier que l'échantillon d'où provient la valeur observée est constitué fortuitement d'individus normaux dont la taille est exceptionnelle. La moyenne ainsi obtenue est peu probable mais toujours possible sous la courbe. Dans ce cas, l'expérimentateur va conclure erronément que l'échantillon n'appartient pas à la population centrée sur µ.

 

2. Voir un effet qui existe:

Si la moyenne observée est comprise dans la zone alpha, cela peut signifier aussi que l'échantillon d'où provient la valeur observée est constitué d'individus appartenant à une population de moyenne (µ1) distincte de µ (en rouge: cas où il existe une population centrée sur une moyenne µ1 plus grande que µ).