1. Savoir d'où l'on part et ce qu'on souhaite démontrer:

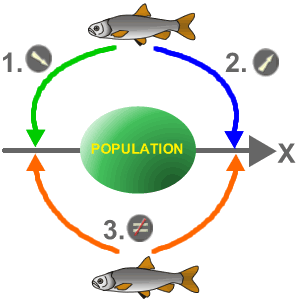
Un expérimentateur a mesuré un chevaine de 3 ans et veut le comparer à la population de chevaines de 3 ans centrée sur µ. Son point de départ est de dire que l'individu est conforme à cette population: c'est l'hypothèse nulle H0. Ce qu'il veut démontrer est SOIT:

1. que le poisson mesuré est plus petit que prédit par la normale et appartient à une population centrée sur µ1 plus petite que µ (en vert)
2. que le poisson mesuré est plus grand que prédit par la normale et appartient à une population centrée sur µ1 plus grande que µ (en bleu)
3. que le poisson mesuré est ou plus grand ou plus petit (DIFFÉRENT) que prédit par le modèle et appartient à une population centrée sur µ1 plus grande OU plus petite que µ (en orange)

H0: µ =µ1
H1:	µ1 inférieure à µ µ1 supérieure à µ µ1 différente de µ

 

2. Convertir la valeur observée en une valeur réduite:

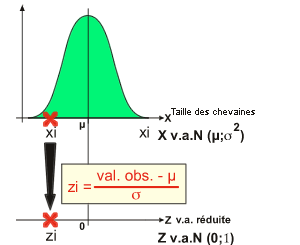
L'expérimentateur a obtenu une taille pour le poisson capturé (ou une taille moyenne s'il en a capturé plusieurs). Pour faciliter sa prise de décision (Accepter le fait que ce poisson est normal [AH0] ou non [RH0]), il va réduire la valeur observée en une valeur réduite (z réduit, t réduit, ...).

 

3. Rechercher dans les tables réduites correspondantes la ou les valeurs seuil:

En fonction du alpha déterminé par l'expérimentateur, il va définir un seuil de signification particulier.

	Test unidirectionnel à droite: Z (1-α)
	Test unidirectionnel à gauche: Z α
	Test bidirectionnel: Z α/2 ou Z (1-α/2)

Exemple: Soit une différence à mettre en évidence pour un alpha de 5% (test bidirectionnel: d'où il y a 2 seuils à trouver Z 0,025 et z0,975) .

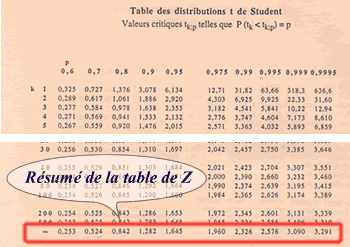
Dans la table de Student (pour rappel (module 70, page 5), la dernière ligne de la table de Student résume la table de Z pour cetaines probabilités, dont toutes celles nécéssaires pour les tests d'hypothèses classiques), on détermine la valeur de z_0,975 (colonne 0,975, ligne z), qui est de 1,96. Par symétrie, on peut déduire le z0,025: -1,96

Conclusion du test:

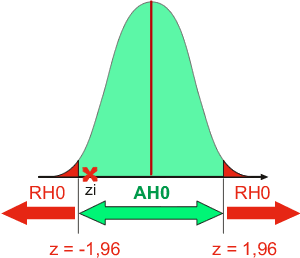
En comparant la valeur réduite des observations (z observé) avec la valeur seuil trouvée dans les tables, l'expérimentateur peut tirer une conclusion à son test.

Exemple: Soit une valeur de z observée de -1,84 pour un test bidirectionnel avec un alpha de 5%. Dans ce cas, -1,84 est compris entre -1,96 et 1,96.

La conclusion au test est la suivante: La mesure observée est normale et obéit aux conditions de l'hypothèse nulle (AH0).

Si la valeur observée n'était pas comprise entre -1,96 et 1,96, l'expérimentateur aurait pu conclure que la mesure observée était différente de la normale et ne répondait plus aux conditions de l'hypothèse nulle (RH0).

 

Remarque:

Dans le cas d'un test bidirectionnel, RH0 signifie bien sûr la mise en évidence d'une différence de la valeur observée par rapport à la normale MAIS on peut aller plus loin. En effet, pour un même alpha MAIS pour un test unidirectionnel, on aura aussi un RH0. L'expérimentateur pourra donc dire qu'il y a une différence de la mesure mais aussi que celle-ci est plus grande ou plus petite que la normale.

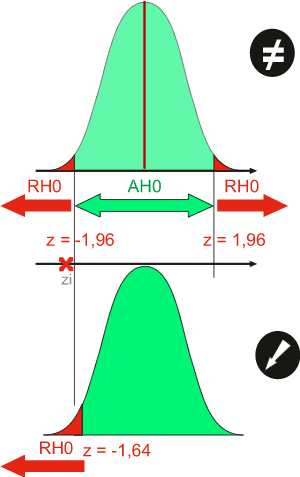
ATTENTION: La conclusion inverse n'est pas vraie. Ce n'est pas parce qu'on observe un RH0 dans un test unidirectionnel avec un alpha déterminé qu'il y a RH0 pour un test bidirectionnel avec le même alpha.