La moyenne d'un échantillon (Mx) n'est pas forcément égale à la moyenne réelle de la population (μ) dont l'échantillon est issu.
Elle s'en rapproche d'autant plus que la taille de l'échantillon (n) est grande.
On peut donc dire que μ = Mx ± ε (ε représentant idéalement une très petite valeur).
La distribution d'échantillonnage de la moyenne Mx, de paramètres (μ;σ2/n), cf. module 70, permet de délimiter autour de Mx une zone dans laquelle μ a, par exemple, 95% de chance de se trouver.
Estimation d'ε :
Lorsque la variance de la population (σ2) est connue, ε est calculé à partir de la valeur de z correspondant à la confiance utilisée:
avec 
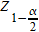la valeur de Z dont la probabilité de lui être inférieur est de 1-α/2.
Estimation de l'intervalle de confiance à 95% :
Estimation précise :
Lorsque la confiance vaut 95% 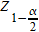vaut Z0,975=1,96.
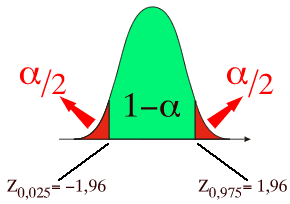
L'intervalle de confiance va donc de :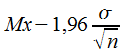 
à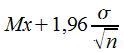 
Estimation approximative :
Lorsque la confiance est de 95%, z = 1,96. On peut donc l'approximer à z=2, et considérer que l'intervalle à 95% a une longueur d'approximativement 4 fois l'écart-type.
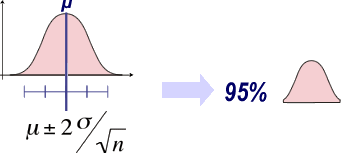
Définir un intervalle de confiance à 95% suppose de raisonner sur une distribution normale tronquée aux deux extrémités, et les affirmations qui suivront n'auront donc que 95% de chance d'être vraies.
La moyenne de l'échantillon Mx étant connue, centrons cet intervalle de 4 fois l'erreur type sur Mx. σ et n étant également connus, les limites de cet intervalle peuvent être facilement calculées :
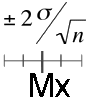
Supposons, dans la distribution tronquée, que Mx est la plus petite possible, puis qu'elle est la plus grande possible :
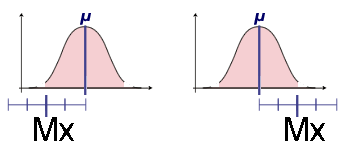
On constate que la moyenne μ se trouve toujours comprise dans l'intervalle Mx ± 2 fois l'erreur type.
La moyenne μ reste inconnue, mais elle se trouve dans des limites connues. Le risque qu'elle se trouve en dehors de ces limites est de 5% si l'intervalle de confiance a été fixé pour une confiance de 95%.
