Le théorème de Bayes permet de déterminer les valeurs prédictives d'un test en connaissant la prévalence de la maladie, la sensibilité et la spécificité du test.

La formule générale du théorème de Bayes peut être retrouvée à partir de la loi des probabilités conditionnelles.

Loi des probabilités conditionnelles: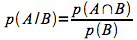

Or, il est possible de décomposer les membres de la fraction:

• au numérateur:
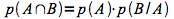
• au dénominateur:

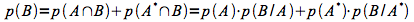
La formule générale du théorème de Bayes est donc:

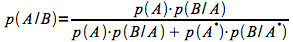
Soient les événements A "être malade " et B "être positif au test" et sachant que p(A) est la prévalence de la maladie (notée p), p(B/A) est la sensibilité et p(B*/A*) est la spécificité, alors le théorème de Bayes, appliqué aux tests diagnostiques, devient:
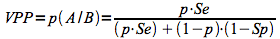
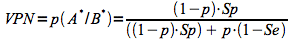