
Les contenus sont © P. Calmant et E. Depiereux - 2004; G. Vincke B. De Hertogh et E. Depiereux 2008.
Imprimé le
12/3/2026
Si on étudie le taux de cholestérol dans le sang , le but est d'analyser les fluctuations de ce taux (notre mesure, notre variable) en fonction:

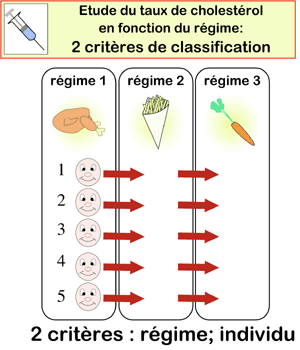
L'expérimentateur constitue plusieurs échantillons contenant des individus pris au hasard dans une population déterminée. L'objectif de l'expérience est de mettre en évidence des différences de taux de cholestérol en fonction du "régime alimentaire". Le critère de classification étudié est unique: il s'agit de "régime alimentaire".
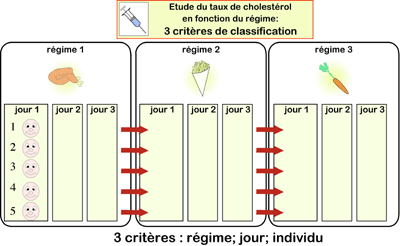
L'expérimentateur constitue plusieurs échantillons à partir des 5 mêmes individus d'une population déterminée. Chaque individu passe successivement par 3 régimes alimentaires. Pour chaque régime, une mesure de taux de cholestérol est réalisée.
L'objectif de l'expérience est de mettre en évidence des différences de taux de cholestérol en fonction du "régime alimentaire". Dans ce cas, il y a deux critères de classification: le critère "régime alimentaire" et le critère "individu" puisque les mesures sont effectuées sur les mêmes individus (1, 2, 3, 4 et 5) pour tous les échantillons.
L'expérimentateur constitue plusieurs échantillons à partir des 5 mêmes individus d'une population déterminée. Chaque individu suit un régime déterminé pendant trois jours avant de passer au régime suivant et ainsi de suite.
L'objectif de l'expérience est de mettre en évidence des différences de taux de cholestérol en fonction du "régime alimentaire" et de la "durée du régime déterminé". Dans ce cas, il y a trois critères de classification: le critère "régime alimentaire", le critère "individu" et le critère "jour".

L'expérience présentée ci-dessus consiste à étudier le taux de cholestérol en fonction d'un régime clairement identifié (régime à base de viande; à base d'aliments à haute teneur en graisses animales; à base de légumes). Le critère "régime" est fixé (connu): le critère est dit "FIXE".

L'expérience présentée ci-dessus consiste à étudier le taux de cholestérol en fonction d'un régime (1, 2 ou 3) non précisé . Le critère "régime" n'est pas fixé (inconnu): il est "ALEATOIRE".
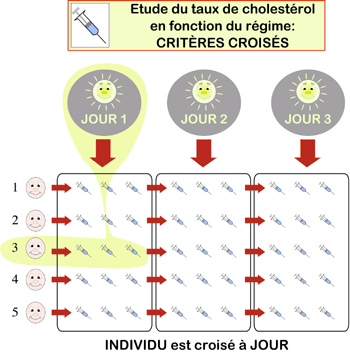
L'expérience présentée ci-dessus consiste à étudier le taux de cholestérol de façon à réaliser 3 prélèvements par jour sur les mêmes individus pendant trois jours. Les individus sont croisés aux jours.
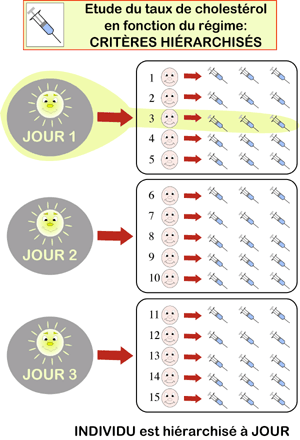
L'expérience présentée ci-dessus consiste à étudier le taux de cholestérol de façon à réaliser 3 prélèvements par jour sur des individus différents de jour en jour. Les individus sont hiérarchisés aux jours.
Afin de compléter l'étude des ANOVA multiples, il est possible d'établir le modèle représentant l'ANOVA moyennant le respect de certaines conventions de notation pour l'écriture du modèle.
Soit X la mesure expérimentale ou observation, µ la moyenne générale de toutes les populations étudiées et E l'erreur résiduelle ou non contrôlée.
Sources de variation:
1. Effets globaux
Soit une ANOVA à trois critères de classification:
Les interactions sont alors:
Le modèle s'écrit donc:
x(ijk)l = µ + ai + B(i)j + ck + acik + Bc(i)jk + E(ijk)l
La SCET se décompose alors comme suit:
SCET = SCEa + SCEB(a) + SCEc + SCEac + SCEBc + SCER
Question: Etablir un schéma des expériences suivantes. Quels sont les critères de classification, combien y a-t-il de niveaux pour chacun des critères? Sont-ils fixes ou aléatoires? Quelles sont les relations entre eux ? Combien y a-t-il de répétitions indépendantes ? Etablir le modèle et l'équation de l'analyse de la variance.
Exemple 1:
Un test hématologique a été effectué sur 5 adultes normaux et 5 adultes atteints d'une maladie sanguine. A chaque individu, on injecte une quantité fixe d'un produit radioactif et on prélève, à différents temps (1, 3, 5 et 10 minutes), un échantillon de sang dont on mesure la radioactivité en cpm (coups par minute).
1' |
3' |
5' |
10' |
||
NORMAUX
|
adulte A |
- |
- |
- |
- |
adulte B |
- |
- |
- |
- |
|
adulte C |
- |
- |
- |
- |
|
adulte D |
- |
- |
- |
- |
|
adulte E |
- |
- |
- |
- |
|
MALADES
|
adulte F |
- |
- |
- |
- |
adulte G |
- |
- |
- |
- |
|
adulte H |
- |
- |
- |
- |
|
adulte I |
- |
- |
- |
- |
|
adulte J |
- |
- |
- |
- |
Effets:
Santé: ai, fixe, croisé avec Temps.
Individu: B(i)j, aléatoire, hiérarchisé à Santé, et croisé avec Temps.
Temps: ck , fixe, croisé avec Santé et Individu.
Interactions:
Entre Santé et Temps: acik
Entre Individu et Temps: Bc(i)jk
Modèle à trois critères de classification, sans répétitions [l=1]
x(ijk)l = µ + ai + B(i)j + ck + acik + Bc(i)jk
SCET = SCEa +SCEB(a) +SCEc + SCEac + SCEBc
Exemple 2:
Une tumeur est prélevée chez 4 souris. De chaque tumeur, on prélève 2 fragments quelconques sur lesquels on dénombre au microscope des cellules particulières. A la suite d'un traitement A, ces comptages ont été effectués à 3 temps successifs (1, 2 et 3 jours après l'administration du traitement) à partir des 4 mêmes souris.
JOUR 1 |
JOUR 2 |
JOUR 3 |
|
SOURIS 1 |
- - |
- - |
- - |
SOURIS 2 |
- - |
- - |
- - |
SOURIS 3 |
- - |
- - |
- - |
SOURIS 4 |
- - |
- - |
- - |
Effets:
Souris: Ai, aléatoire, croisé avec Jours.
Jour: bj, fixe, croisé avec Souris.
Interactions:
Entre Souris et Jour: Abij
Modèle à deux critères de classification, avec 2 répétitions [k=2]
x(ij)k = µ + Ai + bj + Abij + E(ij)k
SCET = SCEA +SCEb +SCEAb + SCER
Problèmes (9 groupes, deux problèmes)
1.1. Dans une étude portant sur la reproduction du goujon, l'impact de trois milieux piscicoles a été examiné : l'étang naturel, un bassin à température constante, un bassin à température et à éclairement constants. Dans chaque milieu, on a mesuré le poids des ovaires de 20 goujons adultes.
2.1. Un test hématologique a été effectué sur 5 adultes normaux et 5 adultes atteints d'une maladie sanguine. A chaque individu, on injecte une quantité fixe d'un produit radioactif et on prélève, à différents temps, un échantillon de sang dont on mesure la radioactivité en cpm.
3.1 Une tumeur est prélevée chez 4 souris. De chaque tumeur, on prélève 2 fragments quelconques sur lesquels on dénombre au microscope des cellules particulières. A la suite d'un traitement A, ces comptages ont été effectués à 3 temps successifs (jour 1, jour 2 et jour 3) à partir des 4 mêmes souris.
4.1 Trois laboratoires désirent comparer leurs résultats d'analyse de calcium dans différentes terres. Quatre prélèvements de terre ont été effectués au hasard dans trois régions, Ardenne, Condroz et Hesbaye. Chaque laboratoire a reçu 1/3 de chaque prélèvement sur lequel il a déterminé la teneur en calcium selon les 2 méthodes (M1 et M2) officiellement reconnues.
5.1 Un ornithologue s'intéresse à l'évolution d'une espèce d'oiseaux répartie dans trois sites géographiquement distincts A, B et C, et plus particulièrement aux différences morphologiques engendrées par les mécanismes d'isolement. A cet effet, il a mesuré la longueur des ailes (en mm) de 10 oiseaux capturés sur chaque site.
6.1 Une industrie pharmaceutique désire tester trois stimulants de l'appétit (S1, S2, S3) en mesurant la capacité d'absorption de nourriture chez le rat. Quatre groupes de 12 rats sont constitués: le premier servant de témoin, les trois autres recevant respectivement les stimulants S1, S2 et S3. On mesure la quantité de nourriture (en kgs) ingérée sur un mois.
7.1 Pour fixer les quotas laitiers, on souhaite réaliser une estimation de la production laitière annuelle d'un cheptel. L'expérimentateur décide de prospecter trois régions au hasard. Dans chaque région, il recueille les statistiques de production de dix vaches prises au hasard, en été et en hiver pour chaque animal.
8.1 Un hydrobiologiste s'intéresse à la teneur en phosphates de deux lacs. A deux saisons différentes, il effectue 5 mesures indépendantes de la concentration en phosphates (microgrammes par litre)
9.1 Un biochimiste étudie l'influence de l'éthanol sur la teneur en graisse dans le foie chez le rat. Il constitue deux groupes de 5 rats: le premier reçoit une ration alimentaire normale et le second reçoit une ration alimentaire à laquelle il ajoute quotidiennement une quantité fixe d'alcool. Après quinze jours, il prélève le foie aux rats, l'homogénéise et y mesure la teneur en graisse sur 3 échantillons d'un gramme.
1.2 Un biochimiste désire comparer deux méthodes de dosage d'une enzyme hépatique. Il prélève le foie à 6 rats et sur chaque foie, après homogénéisation, il prend 4 échantillons dont deux sont analysés par la méthode I et les deux autres par la méthode II.
2.2 Dans un département où coexistent trois variétés d'une même plante, un laboratoire de botanique a étudié si la concentration en chlorophylle des feuilles dépendait de la variété et de l'avancement de la saison. Par variété et par mois, on a mesuré la concentration en chlorophylle sur quatre plantes.
3.2. Un expérimentateur désire tester deux drogues quant à leur effet sur le nombre de lymphocytes chez la souris. Il choisit au sein de 7 portées (une portée = des souris issues de même père et mère), 3 souris, la première servant de contrôle, les deux autres recevant respectivement les drogues A et B. Après quelque temps, il mesure le nombre de lymphocytes en milliers par mm3 de sang.
4.2. Un laboratoire d'analyse de terres désire comparer trois types de sondes pédologiques (S1, S2 et S3) dans les deux types de sols de la région. A cette fin, il prélève 4 échantillons par type de sol et par sonde et mesure le P2O5 dans chaque échantillon de terre.
5.2. Afin de déterminer les facteurs agissant sur la production d'interféron par les lymphocytes, on a planifié l'expérience suivante: quatre taureaux géniteurs de race Pie Rouge sont croisés chacun avec 5 vaches. Sur le veau issu de chaque croisement, on effectue un prélèvement de sang dont on isole les lymphocytes. La moitié des lymphocytes obtenus est stimulée par la lectine CON A et l'autre moitié par la lectine PHA. Après un certain temps, on mesure la quantité d'interféron produite.
6.2. Dans l'étude écologique d'une rivière, 5 stations ont été choisies aléatoirement en amont d'une ville, et 5 stations ont été choisies aléatoirement en aval. Dans chaque station au mois de juillet et au mois d'octobre, on effectue 5 prélèvements d'eau dont on mesure le pH.
7.2. Dans les serres modernes, il est possible d'obtenir un air climatisé dont la température et l'humidité sont contrôlées de façon précise. Dans le but d'étudier l'effet de la vitesse de l'air pulsé sur la croissance de deux espèces florales, l'expérience suivante a été réalisée:trois serres identiques ont été réglées à des vitesses d'air pulsé différentes: V1, V2 et V3. Craignant un effet "paroi", on a mesuré la croissance des plantes à deux endroits différents: au centre et sur le bord sud. A chaque endroit, on mesure après 4 jours, la vitesse de croissance de 10 plantes de chaque espèce.
8.2. Afin de déterminer les facteurs agissant sur la production d'interféron par les lymphocytes, l'expérience suivante a été réalisée: 4 taureaux géniteurs sont choisis respectivement pour la race Pie Rouge et pour la race Bleu Blanc Belge. Chaque taureau est croisé à 5 vaches. Sur le veau issu de chaque croisement, on prélève 3 échantillons de sang dont on mesure la quantité d'interféron produite par les lymphocytes.
9.2. Un vétérinaire désire tester l'action de deux vermifuges sur la croissance pondérale de bovins. Dans un cheptel infesté, il constitue 3 groupes de 15 taurillons: le premier sert de groupe témoin, le deuxième reçoit le vermifuge 1 et le troisième le vermifuge 2. Chaque mois (de novembre à février), chaque animal passe à la pesée et l'on mesure son accroissement en poids en kilos.
Bonus. Un vétérinaire désire tester l'action de deux vermifuges sur la croissance pondérale de bovins. Dans un cheptel infesté, il constitue 4 groupes de 15 taurillons: le premier reçoit le vermifuge 1 à la dose de 200 mgr/kg/jour, le deuxième reçoit le vermifuge 1 à la dose de 400 mgr/kg/jour, le troisième reçoit le vermifuge 2 à la dose de 200 mgr/kg/jour et le quatrième reçoit le vermifuge 2 à la dose de 400 mgr/kg/jour. Chaque mois (de novembre à février), chaque animal passe à la pesée et l'on mesure son accroissement en poids en kilos.
2.
Un test hématologique a été effectué sur 5 adultes normaux et 5 adultes atteints d'une maladie sanguine. A chaque individu, on injecte une quantité fixe d'un produit radioactif et on prélève, à différents temps (1, 3 et 5 minutes), un échantillon de sang dont on mesure la radioactivité en cpm (coups par minute). réponse
3.
Une tumeur est prélevée chez 4 souris. De chaque tumeur, on prélève 2 fragments quelconques sur lesquels on dénombre au microscope des cellules particulières. A la suite d'un traitement A, ces comptages ont été effectués à 3 temps successifs (1, 2 et 3 jours après l'administration du traitement) sur chaque fragment. réponse
4.
Trois laboratoires désirent comparer leurs résultats d'analyse de calcium dans différentes terres. Quatre prélèvements de terre ont été effectués au hasard dans trois régions, Ardenne, Condroz et Hesbaye. Chaque laboratoire a reçu 1/3 de chaque prélèvement sur lequel il a déterminé la teneur en calcium selon les 2 méthodes (M1 et M2) officiellement reconnues. réponse
5.
Un ornithologue s'intéresse à l'évolution d'une espèce d'oiseaux répartie dans trois sites géographiquement distincts (l'observatoire des fagnes, le zwin, et les lacs de l'Eau d'Heure), et plus particulièrement aux différences morphologiques engendrées par les mécanismes d'isolement. A cet effet, il a mesuré la longueur des ailes (en mm) de 10 oiseaux capturés sur chaque site. réponse
6.
Une industrie pharmaceutique désire tester trois stimulants de l'appétit (S1, S2, S3) en mesurant la capacité d'absorption de nourriture chez le rat. Quatre groupes de 12 rats sont constitués: le premier servant de témoin, les trois autres recevant respectivement les stimulants S1, S2 et S3. On mesure la quantité de nourriture (en kg) ingérée sur un mois. réponse
7.
Pour fixer les quotas laitiers, on souhaite réaliser une estimation de la production laitière annuelle d'un cheptel. L'expérimentateur décide de prospecter trois régions au hasard. Dans chaque région, il recueille les statistiques de production de dix vaches prises au hasard, en été et en hiver pour chaque animal. réponse
8.
Un hydrobiologiste s'intéresse à la teneur en phosphates de deux lacs (Lac de Buchenwald, Lac principal des barrages de l'Eau d'Heure). A deux saisons différentes (été, hiver), il effectue 5 mesures indépendantes de la concentration en phosphates (microgrammes par litre). réponse
9.
Un biochimiste étudie l'influence de l'éthanol sur la teneur en graisse dans le foie chez le rat. Il constitue deux groupes de 5 rats: le premier reçoit une ration alimentaire normale et le second reçoit une ration alimentaire à laquelle il ajoute quotidiennement une quantité fixe d'alcool. Après quinze jours, il prélève le foie aux rats, l'homogénéise et y mesure la teneur en graisse sur 3 échantillons d'un gramme. réponse
10.
Un biochimiste désire comparer deux méthodes de dosage d'une enzyme hépatique. Il prélève le foie à 6 rats et sur chaque foie, après homogénéisation, il prend 4 échantillons dont deux sont analysés par la méthode I et les deux autres par la méthode II. réponse
11.
Dans une des serres du département de botanique, plusieurs variétés de bananier coexistent. Pour étudier si la concentration en chlorophylle des feuilles de bananier dépendait de la variété et de l'avancement de la saison, un étudiant, sur la période allant de mars à juin, a choisi 3 variétés au hasard, et pour chacune d'entre elles, a mesuré chaque mois la concentration en chlorophylle sur quatre plantes.
Rédigez le modèle dans le cas où les plantes sont différentes chaque mois, puis dans celui ou elles sont chaque fois identiques. réponse
12.
Un chercheur désire tester deux nouvelles molécules (XB512, XZ321) potentiellement immuno-stimulantes quant à leur effet sur le nombre de lymphocytes chez la souris. Il choisit au sein de 7 portées (une portée = des souris issues de même père et de même mère), 3 souris, la première servant de contrôle, les deux autres recevant respectivement les deux molécules à tester. Après quelque temps, il mesure le nombre de lymphocytes en milliers par mm3 de sang. réponse
13.
Un laboratoire d'analyse de terres désire comparer trois types de sondes pédologiques (S1, S2 et S3) dans les deux types de sols de la région (sableuse, argileuse). A cette fin, il prélève 4 échantillons par type de sol et par sonde et mesure le P2O5 dans chaque échantillon de terre. réponse
14.
Afin de déterminer les facteurs agissant sur la production d'interféron β par les lymphocytes bovins, on a planifié l'expérience suivante: quatre taureaux géniteurs de race Pie Rouge sont croisés chacun avec 5 vaches. Sur le veau issu de chaque croisement, on effectue un prélèvement de sang dont on isole les lymphocytes. La moitié des lymphocytes obtenus est stimulée par la lectine CON A et l'autre moitié par la lectine PHA. Après un certain temps, on mesure la quantité d'interféron β produite. réponse
15.
Dans l'étude écologique d'une rivière, 5 stations ont été choisies aléatoirement en amont d'une ville, et 5 stations ont été choisies aléatoirement en aval. Dans chaque station au mois de juillet et au mois d'octobre, on effectue 5 prélèvements d'eau dont on mesure le pH. réponse
16.
Dans les serres modernes, il est possible d'obtenir un air climatisé dont la température et l'humidité sont contrôlées de façon précise. Dans le but d'étudier l'effet de la vitesse de l'air pulsé sur la croissance de deux espèces florales (Strelitzia reginae et
Beloperone guttata), l'expérience suivante a été réalisée:trois serres identiques ont été réglées à des vitesses d'air pulsé différentes: V1, V2 et V3. Craignant un effet "paroi", on a mesuré la croissance des plantes à deux endroits différents: au centre et sur le bord sud. A chaque endroit, on mesure après 4 jours, la vitesse de croissance de 10 plantes de chaque espèce. réponse
17.
Afin de déterminer les facteurs agissant sur la production d'interféron β par les lymphocytes, l'expérience suivante a été réalisée: 4 taureaux géniteurs de race Pie Rouge et 4 taureaux de race Blanc Bleu Belge ont été sélectionnés. Chaque taureau est croisé avec 5 vaches. Sur le veau issu de chaque croisement, on prélève 3 échantillons de sang dont on mesure la quantité d'interféron β produite par les lymphocytes. réponse
18.
Un vétérinaire désire tester l'action de deux vermifuges sur la croissance pondérale de bovins. Dans un cheptel infesté, il constitue 3 groupes de 15 taurillons: le premier sert de groupe témoin, le deuxième reçoit le vermifuge 1 et le troisième le vermifuge 2. Chaque mois (de novembre à février), chaque animal passe à la pesée et l'on mesure son accroissement en poids en kilos. réponse
19.
Un vétérinaire désire tester l'action de deux vermifuges sur la croissance pondérale de bovins. Dans un cheptel infesté, il constitue 4 groupes de 15 taurillons: le premier reçoit le vermifuge 1 à la dose de 200 mgr/kg/jour, le deuxième reçoit le vermifuge 1 à la dose de 400 mgr/kg/jour, le troisième reçoit le vermifuge 2 à la dose de 200 mgr/kg/jour et le quatrième reçoit le vermifuge 2 à la dose de 400 mgr/kg/jour. Chaque mois (de novembre à février), chaque animal passe à la pesée et l'on mesure son accroissement en poids en kilos. réponse
1. Dans une étude portant sur la reproduction du goujon, l'impact de trois milieux piscicoles a été examiné : l'étang naturel, un bassin à température constante, un bassin à température et à éclairement constants. Dans chaque milieu, on a mesuré le poids des ovaires de 20 goujons adultes.
| Bassin1 | Bassin2 | Bassin3 |
| x11 | x12 | x13 |
| ... | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
| x20 1 | x20 2 | x20 3 |
Anova 1:
Effet "milieu piscicole": fixe, 3 niveaux: ai
Effet résiduel: aléatoire, 20 niveaux: E(i)j
x(i)j= µ + ai + E(i)j
2. Un test hématologique a été effectué sur 5 adultes normaux et 5 adultes atteints d'une maladie sanguine. A chaque individu, on injecte une quantité fixe d'un produit radioactif et on prélève, à différents temps (1, 3 et 5 minutes), un échantillon de sang dont on mesure la radioactivité en cpm (coups par minute).
| 1' | 3' | 5' | ||
| Sains | Individu1 | - | - | - |
| Individu2 | - | - | - | |
| Individu3 | - | - | - | |
| Individu4 | - | - | - | |
| Individu5 | - | - | - | |
| Malades | Individu6 | - |
- | - |
| Individu7 | - | - | - | |
| Individu8 | - | - | - | |
| Individu9 | - | - | - | |
| Individu10 | - | - | - |
Anova 3:
Effet "maladie" : fixe, 2 niveaux : ai
Effet "individus": aléatoire, hiérarchisé à "maladie", 5 niveaux par niveau de "maladie" :B(i)j
Effet "temps": fixe, 3 niveaux : ck
Interaction entre "maladie" et "temps" : acik
Interaction entre "individus" et "temps" : Bc(i)jk
Pas d'effet résiduel car 1 seule mesure par catégorie (l=1).
x(ijk)l = µ + ai + B(i)j + ck + acik + Bc(i)jk
3. Une tumeur est prélevée chez 4 souris. De chaque tumeur, on prélève 2 fragments quelconques sur lesquels on dénombre au microscope des cellules particulières. A la suite d'un traitement A, ces comptages ont été effectués à 3 temps successifs (1, 2 et 3 jours après l'administration du traitement) sur chaque fragment.
Si on considère que les fragments ne sont pas homogènes :
Jour 1 |
Jour 2 |
Jour 3 |
||
Souris1 |
Fragment1 |
- |
- |
- |
Fragment2 |
- |
- |
- |
|
Souris2 |
Fragment3 |
- |
- |
- |
Fragment4 |
- |
- |
- |
|
Souris3 |
Fragment5 |
- |
- |
- |
Fragment6 |
- |
- |
- |
|
Souris4 |
Fragment7 |
- |
- |
- |
Fragment8 |
- |
- |
- |
Anova 3:
Effet "souris" : aléatoire, 4 niveaux : Ai
Effet "fragment": aléatoire, hiérarchisé à "souris", 2 niveaux par niveau de "souris" : B(i)j
Effet "temps": fixe, 3 niveaux : ck
Interaction entre "souris" et "temps" : Acik
Interaction entre "fragment" et "temps" : Bc(i)jk
Pas d'effet résiduel car 1 seule mesure par catégorie (l=1).
x(ijk)l = µ + Ai + B(i)j + ck + Acik + Bc(i)jk
Si on considère que les fragments sont homogènes :
Jour 1 |
Jour 2 |
Jour 3 |
|
Souris1 |
- - |
- - |
- - |
Souris2 |
- - |
- - |
- - |
Souris3 |
- - |
- - |
- - |
Souris4 |
- - |
- - |
- - |
Anova 2:
Effet "souris" : aléatoire, 4 niveaux : Ai
Effet "temps": fixe, 3 niveaux : b j
Interaction entre "souris" et "temps" : Abij
Effet résiduel car 2 mesures par catégorie (k=2): E(ij)k
x(ij)k = µ + Ai + bj + Abij + E(ij)k
4. Trois laboratoires désirent comparer leurs résultats d'analyse de calcium dans différentes terres. Quatre prélèvements de terre ont été effectués au hasard dans trois régions, Ardenne, Condroz et Hesbaye. Chaque laboratoire a reçu 1/3 de chaque prélèvement sur lequel il a déterminé la teneur en calcium selon les 2 méthodes officiellement reconnues.
| Labo1 | Labo2 | Labo3 | ||||
| Ardennes | Méth 1 | Méth 2 | Méth 1 | Méth 2 | Méth 1 | Méth 2 |
| Echant1 | - | - | - | - | - | - |
| Echant2 | - | - | - | - | - | - |
| Echant3 | - | - | - | - | - | - |
| Echant4 | - | - | - | - | - | - |
| Condroz | ||||||
| Echant5 | - | - | - | - | - | - |
| Echant6 | - | - | - | - | - | - |
| Echant7 | - | - | - | - | - | - |
| Echant8 | - | - | - | - | - | - |
| Hesbaye | ||||||
| Echant9 | - | - | - | - | - | - |
| Echant10 | - | - | - | - | - | - |
| Echant11 | - | - | - | - | - | - |
| Echant12 | - | - | - | - | - | - |
Anova 4:
Effet "région" : fixe, 3 niveaux : ai
Effet "échantillon": aléatoire, hiérarchisé à "région", 4 niveaux par niveau de "région" : B(i)j
Effet "labo": fixe, 3 niveaux : ck
Effet "méthode": fixe, 2 niveaux : dl
Interaction entre "région" et "labo" : acik
Interaction entre "région" et "méthode": adil
Interaction entre "échantillon" et "labo" : Bc(i)jk
Interaction entre "échantillon" et "méthode": Bd(i)jl
Interaction entre "labo" et "méthode": cdkl
Interaction entre "région", "labo", et "méthode": acdikl
Interaction entre "échantillon", "labo", et "méthode": Bcd(i)jkl
Pas d'effet résiduel car 1 seule mesure par catégorie (n=1).
x(ijkl)n = µ + ai + B(i)j + ck + dl + acik + adil + Bc(i)jk + Bd(i)jl + cdkl + acdikl + Bcd(i)jkl
5. Un ornithologue s'intéresse à l'évolution d'une espèce d'oiseaux répartie dans trois sites géographiquement distincts (l'observatoire des fagnes, le zwin, et les lacs de l'Eau d'Heure), et plus particulièrement aux différences morphologiques engendrées par les mécanismes d'isolement. A cet effet, il a mesuré la longueur des ailes (en mm) de 10 oiseaux capturés sur chaque site.
Fagnes |
Zwin |
Eau d'Heure |
Oiseau1 |
Oiseau11 |
Oiseau21 |
Oiseau2 |
Oiseau12 |
Oiseau22 |
Oiseau3 |
Oiseau13 |
Oiseau23 |
Oiseau4 |
Oiseau14 |
Oiseau24 |
Oiseau5 |
Oiseau15 |
Oiseau25 |
Oiseau6 |
Oiseau16 |
Oiseau26 |
Oiseau7 |
Oiseau17 |
Oiseau27 |
Oiseau8 |
Oiseau18 |
Oiseau28 |
Oiseau9 |
Oiseau19 |
Oiseau29 |
Oiseau10 |
Oiseau20 |
Oiseau30 |
Anova 1:
Effet "site géographique ": fixe, 3 niveaux: ai
Effet résiduel: aléatoire, 10 niveaux: E(i)j
x(i)j = µ + ai + E(i)j
6. Une industrie pharmaceutique désire tester trois stimulants de l'appétit (S1, S2, S3) en mesurant la capacité d'absorption de nourriture chez le rat. Quatre groupes de 12 rats sont constitués: le premier servant de témoin, les trois autres recevant respectivement les stimulants S1, S2 et S3. On mesure la quantité de nourriture (en kgs) ingérée sur un mois.
Témoin |
Stimul 1 |
Stimul 2 |
Stimul 3 |
Rat1 |
Rat13 |
Rat25 |
Rat37 |
Rat2 |
Rat14 |
Rat26 |
Rat38 |
Rat3 |
Rat15 |
Rat27 |
Rat39 |
Rat4 |
Rat16 |
Rat28 |
Rat40 |
Rat5 |
Rat17 |
Rat29 |
Rat41 |
Rat6 |
Rat18 |
Rat30 |
Rat42 |
Rat7 |
Rat19 |
Rat31 |
Rat43 |
Rat8 |
Rat20 |
Rat32 |
Rat44 |
Rat9 |
Rat21 |
Rat33 |
Rat45 |
Rat10 |
Rat22 |
Rat34 |
Rat46 |
Rat11 |
Rat23 |
Rat35 |
Rat47 |
Rat12 |
Rat24 |
Rat36 |
Rat48 |
Anova 1:
Effet "stimulant": fixe, 4 niveaux: ai
Effet résiduel: aléatoire, 12 niveaux: E(i)j
x(i)j = µ + ai + E(i)j
7. Pour fixer les quotas laitiers, on souhaite réaliser une estimation de la production laitière annuelle d'un cheptel. L'expérimentateur décide de prospecter trois régions au hasard. Dans chaque région, il recueille les statistiques de production de dix vaches prises au hasard, en été et en hiver pour chaque animal.
Eté |
Hiver |
||
Région1 |
Vache1 |
- |
- |
Vache2 |
- |
- |
|
.. |
- |
- |
|
Vache10 |
- |
- |
|
Région2 |
Vache11 |
- |
- |
Vache12 |
- |
- |
|
.. |
- |
- |
|
Vache20 |
- |
- |
|
Région3 |
Vache21 |
- |
- |
Vache22 |
- |
- |
|
.. |
- |
- |
|
Vache30 |
- |
- |
Anova 3:
Effet "région" : aléatoire, 3 niveaux : Ai
Effet "vache": aléatoire, hiérarchisé à "région", 10 niveaux par niveau de "région" : B(i)j
Effet "saison": fixe, 2 niveaux : ck
Interaction entre "région" et "saison" : Acik
Interaction entre "vache" et "saison" : Bc(i)jk
Pas d'effet résiduel car 1 seule mesure par catégorie (l=1).
x(ijk)l = µ + Ai + B(i)j + ck + Acik + Bc(i)jk
8. Un hydrobiologiste s'intéresse à la teneur en phosphates de deux lacs (Lac de Buchenwald, Lac principal des barrages de l'Eau d'Heure). A deux saisons différentes (été, hiver), il effectue 5 mesures indépendantes de la concentration en phosphates (microgrammes par litre).
Saison1 |
Saison2 |
|
Buchenwald |
- |
- |
- |
- |
|
- |
- |
|
- |
- |
|
- |
- |
|
Eau d'Heure |
- |
- |
- |
- |
|
- |
- |
|
- |
- |
|
- |
- |
Anova 2:
Effet "lac": fixe, 2 niveaux: ai
Effet "saison": fixe, 2 niveaux: bj
Interaction entre "lac" et "saison": abij
Effet résiduel: aléatoire, 5 niveaux: E(ij)k
x(ij)k = µ + ai + bj + abij + E(ij)k
9. Un biochimiste étudie l'influence de l'éthanol sur la teneur en graisse dans le foie chez le rat. Il constitue deux groupes de 5 rats: le premier reçoit une ration alimentaire normale et le second reçoit une ration alimentaire à laquelle il ajoute quotidiennement une quantité fixe d'alcool. Après quinze jours, il prélève le foie aux rats, l'homogénéise et y mesure la teneur en graisse sur 3 échantillons d'un gramme.
Témoin |
Rat1 |
- |
- |
- |
Rat2 |
- |
- |
- |
|
Rat3 |
- |
- |
- |
|
Rat4 |
- |
- |
- |
|
Rat5 |
- |
- |
- |
|
Alcool |
Rat6 |
- |
- |
- |
Rat7 |
- |
- |
- |
|
Rat8 |
- |
- |
- |
|
Rat9 |
- |
- |
- |
|
Rat10 |
- |
- |
- |
Anova 2:
Effet "régime": fixe, 2 niveaux: ai
Effet "rat": aléatoire, hiérarchisé à "régime", 5 niveaux: B(i)j
Effet résiduel: aléatoire, 3 niveaux: E(ij)k
x(ij)k= µ + ai + B(i)j + E(ij)k
10. Un biochimiste désire comparer deux méthodes de dosage d'une enzyme hépatique. Il prélève le foie à 6 rats et sur chaque foie, après homogénéisation, il prend 4 échantillons dont deux sont analysés par la méthode I et les deux autres par la méthode II.
Méthode1 |
Méthode2 |
|
Rat1 |
- |
- |
- |
- |
|
Rat2 |
- |
- |
- |
- |
|
Rat3 |
- |
- |
- |
- |
|
Rat4 |
- |
- |
- |
- |
|
Rat5 |
- |
- |
- |
- |
|
Rat6 |
- |
- |
- |
- |
Anova 2:
Effet "rat": aléatoire, 6 niveaux: Ai
Effet "méthode": fixe, 2 niveaux: bj
Interaction entre "rat" et "méthode": Abij
Effet résiduel: aléatoire, 2 niveaux: E(ij)k
x(ij)k= µ + Ai + bj + Abij + E(ij)k
11. Dans une des serres du département de botanique, plusieurs variétés de bananier coexistent. Pour étudier si la concentration en chlorophylle des feuilles de bananier dépendait de la variété et de l'avancement de la saison, un étudiant, sur la période allant de mars à juin, a choisi 3 variétés au hasard, et pour chacune d'entre elles, a mesuré chaque mois la concentration en chlorophylle sur quatre plantes.
Si les plantes sont différentes chaque mois:
Mois1 |
Mois2 |
Mois3 |
Mois4 |
|
Variété1 |
Plante1 |
Plante13 |
Plante25 |
Plante36 |
Plante2 |
Plante14 |
Plante26 |
Plante37 |
|
Plante3 |
Plante15 |
Plante27 |
Plante38 |
|
Plante4 |
Plante16 |
Plante28 |
Plante39 |
|
Variété2 |
Plante5 |
Plante17 |
Plante29 |
Plante40 |
Plante6 |
Plante18 |
Plante30 |
Plante41 |
|
Plante7 |
Plante19 |
Plante31 |
Plante42 |
|
Plante8 |
Plante20 |
Plante32 |
Plante43 |
|
Variété3 |
Plante9 |
Plante21 |
Plante33 |
Plante44 |
Plante10 |
Plante22 |
Plante34 |
Plante45 |
|
Plante11 |
Plante23 |
Plante35 |
Plante46 |
|
Plante12 |
Plante24 |
Plante36 |
Plante47 |
Anova 2:
Effet "variété": aléatoire, 3 niveaux: Ai
Effet "mois": fixe, 4 niveaux: bj
Interaction entre "variété" et "mois": Abij
Effet résiduel: aléatoire, 4 niveaux: E(ij)k
x(ij)k = µ + Ai + bj + Abij + E(ij)k
Si les plantes sont identiques chaque mois:
Mois1 |
Mois2 |
Mois3 |
Mois4 |
||
Variété1 |
Plante1 |
- |
- |
- |
- |
Plante2 |
- |
- |
- |
- |
|
Plante3 |
- |
- |
- |
- |
|
Plante4 |
- |
- |
- |
- |
|
Variété2 |
Plante5 |
- |
- |
- |
- |
Plante6 |
- |
- |
- |
- |
|
Plante7 |
- |
- |
- |
- |
|
Plante8 |
- |
- |
- |
- |
|
Variété3 |
Plante9 |
- |
- |
- |
- |
Plante10 |
- |
- |
- |
- |
|
Plante11 |
- |
- |
- |
- |
|
Plante12 |
- |
- |
- |
- |
Anova 3:
Effet "variété": aléatoire, 3 niveaux: Ai
Effet "plante": aléatoire, hiérarchisé à "variété", 4 niveaux: B(i)j
Effet "mois": fixe, 4 niveaux : ck
Interaction entre "variété" et "mois" : Acik
Interaction entre "plante" et "mois" : Bc(i)jk
Pas d'effet résiduel car 1 seule mesure par catégorie (l=1).
x(ijk)l = µ + Ai + B(i)j + ck + Acik + Bc(i)jk
12. Un chercheur désire tester deux nouvelles molécules (XB512, XZ321) potentiellement immuno-stimulantes quant à leur effet sur le nombre de lymphocytes chez la souris. Il choisit au sein de 7 portées (une portée = des souris issues de même père et de même mère), 3 souris, la première servant de contrôle, les deux autres recevant respectivement les deux molécules à tester. Après quelque temps, il mesure le nombre de lymphocytes en milliers par mm3 de sang.
Portée1 |
Portée2 |
Portée3 |
Portée4 |
Portée5 |
Portée6 |
Portée7 |
|
Contrôle |
Rat1 |
Rat4 |
Rat7 |
Rat10 |
Rat13 |
Rat16 |
Rat19 |
XB512 |
Rat2 |
Rat5 |
Rat8 |
Rat11 |
Rat14 |
Rat17 |
Rat20 |
XZ321 |
Rat3 |
Rat6 |
Rat9 |
Rat12 |
Rat15 |
Rat18 |
Rat21 |
Anova 2:
Effet "molécule": fixe, 3 niveaux: ai
Effet "Portée": aléatoire, 7 niveaux: Bj
Interaction entre "molécule" et "portée": aBij
Pas d'effet résiduel car 1 seule mesure par catégorie (k=1).
x(ij)k= µ + ai + Bj + aBij
13. Un laboratoire d'analyse de terres désire comparer trois types de sondes pédologiques (S1, S2 et S3) dans les deux types de sols de la région (sableuse, argileuse). A cette fin, il prélève 4 échantillons par type de sol et par sonde et mesure le P2O5 dans chaque échantillon de terre.
sableuse |
argileuse |
|
Sonde1 |
Echant 1 |
Echant 13 |
Echant 2 |
Echant 14 |
|
Echant 3 |
Echant 15 |
|
Echant 4 |
Echant 16 |
|
Sonde2 |
Echant 5 |
Echant 17 |
Echant 6 |
Echant 18 |
|
Echant 7 |
Echant 19 |
|
Echant 8 |
Echant 20 |
|
Sonde3 |
Echant 9 |
Echant 21 |
Echant 10 |
Echant 22 |
|
Echant 11 |
Echant 23 |
|
Echant 12 |
Echant 24 |
Anova 2:
Effet "sonde": fixe, 3 niveaux: ai
Effet "terre": fixe, 2 niveaux: bj
Interaction entre "sonde" et "terre ": abij
Effet résiduel: aléatoire, 4 niveaux: E(ij)k
x(ij)k= µ + ai + bj + abij + E(ij)k
14. Afin de déterminer les facteurs agissant sur la production d'interféron β par les lymphocytes bovins, on a planifié l'expérience suivante: quatre taureaux géniteurs de race Pie Rouge sont croisés chacun avec 5 vaches. Sur le veau issu de chaque croisement, on effectue un prélèvement de sang dont on isole les lymphocytes. La moitié des lymphocytes obtenus est stimulée par la lectine CON A et l'autre moitié par la lectine PHA. Après un certain temps, on mesure la quantité d'interféron β produite.
Lectine ConA |
Lectine PHA |
||
Taureau1 |
Vache1 |
- |
- |
Vache2 |
- |
- |
|
Vache3 |
- |
- |
|
Vache4 |
- |
- |
|
Vache5 |
- |
- |
|
Taureau2 |
Vache6 |
- |
- |
Vache7 |
- |
- |
|
Vache8 |
- |
- |
|
Vache9 |
- |
- |
|
Vache10 |
- |
- |
|
Taureau3 |
Vache11 |
- |
- |
Vache12 |
- |
- |
|
Vache13 |
- |
- |
|
Vache14 |
- |
- |
|
Vache15 |
- |
- |
|
Taureau4 |
Vache16 |
- |
- |
Vache17 |
- |
- |
|
Vache18 |
- |
- |
|
Vache19 |
- |
- |
|
Vache20 |
- |
- |
Anova 3:
Effet "taureau": aléatoire, 4 niveaux: Ai
Effet "vache": aléatoire, hiérarchisé à "taureau", 5 niveaux: B(i)j
Effet "lectine": fixe, 2 niveaux : ck
Interaction entre "taureau" et "lectine" : Acik
Interaction entre "vache" et "lectine" : Bc(i)jk
Pas d'effet résiduel car 1 seule mesure par catégorie (l=1).
x(ijk)l = µ + Ai + B(i)j + ck + Acik + Bc(i)jk
15. Dans l'étude écologique d'une rivière, 5 stations ont été choisies aléatoirement en amont d'une ville, et 5 stations ont été choisies aléatoirement en aval. Dans chaque station au mois de juillet et au mois d'octobre, on effectue 5 prélèvements d'eau dont on mesure le pH.
Juillet |
Octobre |
||
Amont |
Station1 |
5 |
5 |
Station2 |
5 |
5 |
|
Station3 |
5 |
5 |
|
Station4 |
5 |
5 |
|
Station5 |
5 |
5 |
|
Aval |
Station6 |
5 |
5 |
Station7 |
5 |
5 |
|
Station8 |
5 |
5 |
|
Station9 |
5 |
5 |
|
Station10 |
5 |
5 |
Anova 3:
Effet "amont/aval": fixe, 2 niveaux: ai
Effet "station": aléatoire, hiérarchisé à "amont/aval", 5 niveaux: B(i)j
Effet "mois": fixe, 2 niveaux : ck
Interaction entre "amont/aval" et "mois" : acik
Interaction entre "station" et "mois" : Bc(i)jk
Effet résiduel: aléatoire, 5 niveaux: E(ijk)l
x(ijk)l = µ + ai + B(i)j + ck + acik + Bc(i)jk + E(ijk)l
16. Dans les serres modernes, il est possible d'obtenir un air climatisé dont la température et l'humidité sont contrôlées de façon précise. Dans le but d'étudier l'effet de la vitesse de l'air pulsé sur la croissance de deux espèces florales (Strelitzia reginae et Beloperone guttata), l'expérience suivante a été réalisée: trois serres identiques ont été réglées à des vitesses d'air pulsé différentes: V1, V2 et V3. Craignant un effet "paroi", on a mesuré la croissance des plantes à deux endroits différents: au centre et sur le bord sud. A chaque endroit, on mesure après 4 jours, la vitesse de croissance de 10 plantes de chaque espèce.
espèce1 |
espèce2 |
|||
Serre1 (vitesse1) |
bord sud |
10 |
10 |
|
Centre |
10 |
10 |
||
Serre2 (vitesse2) |
bord sud |
10 |
10 |
|
Centre |
10 |
10 |
||
Serre3 (vitesse3) |
bord sud |
10 |
10 |
|
Centre |
10 |
10 |
Anova 3:
Effet "vitesse": fixe, 3 niveaux: ai
Effet "localisation": fixe, 2 niveaux: bj
Effet "espèce": fixe, 2 niveaux : ck
Interaction entre "vitesse" et "espèce" : acik
Interaction entre "localisation" et "espèce" : bcjk
Interaction entre "vitesse" et "localisation" : abij
Interaction entre "vitesse", "localisation" et "espèce": abcijk
Effet résiduel: aléatoire, 10 niveaux: E(ijk)l
x(ijk)l = µ + ai + bj + ck + acik + bcjk + + abij + abcijk + E(ijk)l
17. Afin de déterminer les facteurs agissant sur la production d'interféron β par les lymphocytes, l'expérience suivante a été réalisée: 4 taureaux géniteurs de race Pie Rouge et 4 taureaux de race Blanc Bleu Belge ont été sélectionnés. Chaque taureau est croisé avec 5 vaches. Sur le veau issu de chaque croisement, on prélève 3 échantillons de sang dont on mesure la quantité d'interféron β produite par les lymphocytes.
Pie Rouge |
Taureau1 |
Vache 1 |
- |
- |
- |
|
Vache 5 |
- |
- |
- |
|||
Taureau2 |
Vache 6 |
- |
- |
- |
||
Vache 10 |
- |
- |
- |
|||
Taureau3 |
Vache 11 |
- |
- |
- |
||
Vache 15 |
- |
- |
- |
|||
Taureau4 |
Vache 16 |
- |
- |
- |
||
Vache 20 |
- |
- |
- |
|||
BBB |
Taureau5 |
Vache 21 |
- |
- |
- |
|
Vache 25 |
- |
- |
- |
|||
Taureau6 |
Vache 26 |
- |
- |
- |
||
Vache 30 |
- |
- |
- |
|||
Taureau7 |
Vache 31 |
- |
- |
- |
||
Vache 35 |
- |
- |
- |
|||
Taureau8 |
Vache 36 |
- |
- |
- |
||
Vache 40 |
- |
- |
- |
Anova 3:
Effet "race": fixe, 2 niveaux: ai
Effet "taureau": aléatoire, hiérarchisé à "race", 4 niveaux: B(i)j
Effet "vache": aléatoire, hiérarchisé à "taureau", 5 niveaux: C(ij)k
Pas d'interaction car tous hiérarchisés.
Effet résiduel: aléatoire, 3 niveaux: E(ijk)l
x(ijk)l = µ + ai + B(i)j + C(ij)k + E(ijk)l
18. Un vétérinaire désire tester l'action de deux vermifuges sur la croissance pondérale de bovins. Dans un cheptel infesté, il constitue 3 groupes de 15 taurillons: le premier sert de groupe témoin, le deuxième reçoit le vermifuge 1 et le troisième le vermifuge 2. Chaque mois (de novembre à février), chaque animal passe à la pesée et l'on mesure son accroissement en poids en kilos.
Novembre |
Décembre |
Janvier |
Février |
||
Témoin |
Taurillon1 |
- |
- |
- |
- |
Taurillon15 |
- |
- |
- |
- |
|
Vermifuge1 |
Taurillon16 |
- |
- |
- |
- |
Taurillon30 |
- |
- |
- |
- |
|
Vermifuge2 |
Taurillon31 |
- |
- |
- |
- |
Taurillon45 |
- |
- |
- |
- |
Anova 3:
Effet "vermifuge": fixe, 3 niveaux: ai
Effet "taurillon": aléatoire, hiérarchisé à "vermifuge", 15 niveaux: B(i)j
Effet "mois": fixe, 4 niveaux : ck
Interaction entre "vermifuge" et "mois" : acik
Interaction entre "taurillon" et "mois" : Bc(i)jk
Pas d'effet résiduel car 1 seule mesure par catégorie (l=1).
x(ijk)l = µ + ai + B(i)j + ck + acik + Bc(i)jk
19. Un vétérinaire désire tester l'action de deux vermifuges sur la croissance pondérale de bovins. Dans un cheptel infesté, il constitue 4 groupes de 15 taurillons: le premier reçoit le vermifuge 1 à la dose de 200 mgr/kg/jour, le deuxième reçoit le vermifuge 1 à la dose de 400 mgr/kg/jour, le troisième reçoit le vermifuge 2 à la dose de 200 mgr/kg/jour et le quatrième reçoit le vermifuge 2 à la dose de 400 mgr/kg/jour. Chaque mois (de novembre à février), chaque animal passe à la pesée et l'on mesure son accroissement en poids en kilos.
Novembre |
Décembre |
Janvier |
Février |
|||
Dose1 |
Taurillon1 |
- |
- |
- |
- |
|
- |
- |
- |
- |
|||
Taurillon15 |
- |
- |
- |
- |
||
Verm1 |
- |
- |
- |
- |
||
Dose2 |
Taurillon16 |
- |
- |
- |
- |
|
- |
- |
- |
- |
|||
Taurillon30 |
- |
- |
- |
- |
||
- |
- |
- |
- |
|||
Dose1 |
Taurillon31 |
- |
- |
- |
- |
|
- |
- |
- |
- |
|||
Verm2 |
Taurillon45 |
- |
- |
- |
- |
|
Dose2 |
Taurillon46 |
- |
- |
- |
- |
|
- |
- |
- |
- |
|||
Taurillon60 |
- |
- |
- |
- |
Anova 4:
Effet "vermifuge": fixe, 2 niveaux: ai
Effet "dose": fixe, 2 niveaux: bj
Effet "taurillon": aléatoire, hiérarchisé à "dose" et "vermifuge", 15 niveaux : C(ij)k
Effet "mois": fixe, 4 niveaux: dl
Interaction entre "vermifuge" et "dose" : abij
Interaction entre "vermifuge" et "mois" : adil
Interaction entre "dose" et "mois" : bdjl
Interaction entre "taurillon" et "mois" : Cd(ij)kl
Interaction entre "vermifuge", "dose" et "mois" : abdijl
Pas d'effet résiduel car 1 seule mesure par catégorie (m=1).
x(ijkl)m = µ + ai + bj + C(ij)k + dl + abij + adil + bdjl + Cd(ij)kl + abdijl
Erreur !