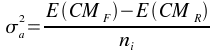
Les contenus sont © P. Calmant et E. Depiereux - 2004; G. Vincke B. De Hertogh et E. Depiereux 2008.
Imprimé le
12/3/2026
L'ANOVA 1 aléatoire s'applique aux échantillonnages à 2 niveaux, c'est-à-dire aux expériences où plusieurs mesures (appelées alors des réplicats) sont réalisées par individu.
Dans ce type d'expérience, nous ne pouvons pas approfondir l'analyse par l'étude des contrastes. Par contre, il est possible de déterminer le nombre de réplicats et d'individus optimaux.
Exemple:
Pour étudier le poids des hommes, on effectue 4 pesées sur 5 hommes pris au hasard dans la population.
mesure |
homme1 |
homme 2 |
homme 3 |
homme 4 |
homme 5 |
1 |
80,0 |
93,2 |
78,3 |
85,1 |
97,2 |
2 |
80,5 |
93,8 |
78,1 |
84,9 |
97,5 |
3 |
79,8 |
92,9 |
78,6 |
85,0 |
97,1 |
4 |
80,2 |
93,4 |
78,2 |
85,3 |
97,4 |
moyenne |
80,125 |
93,325 |
78,300 |
85,075 |
97,300 |
variance |
0,089 |
0,142 |
0,047 |
0,029 |
0,033 |
Premier niveau d'échantillonnage : les individus : le poids est une variable qui suit une distribution normale au sein de la population masculine. Les moyennes de chaque homme suivent donc une distribution normale.
Deuxième niveau d'échantillonnage : les mesures : les 4 mesures (4 réplicats) prises sur un même individu ne seront pas exactement les mêmes, et se distribuent elles aussi selon une distribution normale, mais qui n'est pas la même que celle des individus. Nous observons donc un deuxième niveau de variabilité.
Variance totale = variance des hommes + variance des réplicats
Soit, σ2x = σ2a + σ2
Les calculs de l'ANOVA 1 aléatoire sont les mêmes que lors de la réalisation de l'ANOVA 1 fixe.
variance du premier niveau d'échantillonnage:
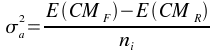
variance du deuxième niveau d'échantillonnage:
![]()
Intervalle de confiance:
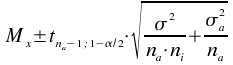
Ce qui
peut être résumé en :
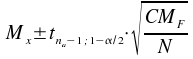
Pour ce calcul on doit d'abord calculer celui du deuxième niveau d'échantillonnage, car cette valeur est nécessaire pour calculer celui du premier niveau.
soit le nombre de réplicats nécessaires :
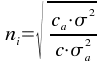
Ca : coût de l'individu
C : coût du réplicat
soit le nombre d'individus nécessaires pour garantir la signification d'une différence Δ :
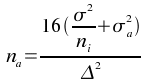
A réaliser dans un fichier Excel.
Pour déterminer le taux de catalase dans le foie de rat, un expérimentateur prélève le foie de 4 rats et réalise 5 dosages sur chaque foie
rat 1 |
rat 2 |
rat 3 |
rat 4 |
113.33 |
114.42 |
130.37 |
127.17 |
119.05 |
111.89 |
133.19 |
128.5 |
117.95 |
113.75 |
130.04 |
125.44 |
124.84 |
105.93 |
130.96 |
125.11 |
103.36 |
116.2 |
137.36 |
121.01 |