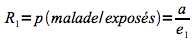
Les contenus sont © P. Calmant et E. Depiereux - 2004; G. Vincke B. De Hertogh et E. Depiereux 2008.
Imprimé le
12/3/2026
Une étude épidémiologique peut être réalisée afin de mettre en évidence un lien entre une maladie et un facteur de risque supposé.
Il existe plusieurs types d'études épidémiologiques dont les études de cohorte et les enquêtes cas-témoins.
Deux groupes de personnes sont constitués: un groupe composé de personnes atteintes de la maladie et un groupe composé de personnes non-atteintes de la maladie (témoins). Le passé de chaque personne est analysé afin de déterminer si elle a été exposée au facteur de risque étudié.
Deux groupes de personnes sont constitués: le premier est composé de personnes exposées à un facteur de risque déterminé tandis que le second comporte des personnes non-exposées à ce facteur de risque. Ces personnes sont suivies durant un certain temps afin de constater si elles développent ou non la maladie étudiée.
Les résultats d'une étude épidémiologique peuvent être représentés sous la forme d'une table de contingence.
Cette table de contingence est similaire à celle utilisée pour résoudre les exercices de probabilités au module 30, mais elle traite des fréquences plutôt que des probabilités.
|
|
||||||||||||||||||||||||||||||||
Soient l'évènement A "être malade" et l'évènement B "être exposé au facteur de risque", alors la table de contingence est adaptée et devient la suivante; avec:
| Malade | Non-malade | ||
|---|---|---|---|
| Exposé | a | b | e1 |
| Non-exposé | c | d | e0 |
| m1 | m0 | N |
Dans une étude de cohorte, les valeurs m1 et m0 sont aléatoires. Elles ne sont donc pas indiquées au niveau de la table de contingence qui devient:
| Malade | Non-malade | ||
|---|---|---|---|
| Exposé | a | b | e1 |
| Non-exposé | c | d | e0 |
Dans une enquête cas-témoins, ce sont les valeurs e1 et e0 qui sont aléatoires. Elles ne sont donc pas indiquées au niveau de la table de contingence qui devient:
| Malade | Non-malade | |
|---|---|---|
| Exposé | a | b |
| Non-exposé | c | d |
| m1 | m0 |
Le risque absolu chez les exposés est la probabilité qu'une personne soit malade sachant qu'elle est exposée au facteur de risque.
Il correspond donc au rapport entre le nombre de personnes malades et exposées et l'ensemble des personnes exposées au facteur de risque.
| Malade | Non-malade | ||
|---|---|---|---|
| Exposé | a | b | e1 |
| Non-exposé | c | d | e0 |
| m1 | m0 | N |
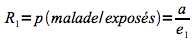
Le risque absolu chez les non-exposés est la probabilité qu'une personne soit malade sachant qu'elle n'est pas exposée au facteur de risque.
Il correspond donc au rapport entre le nombre de personnes malades et non-exposées et l'ensemble des personnes non-exposées au facteur de risque.
| Malade | Non-malade | ||
|---|---|---|---|
| Exposé | a | b | e1 |
| Non-exposé | c | d | e0 |
| m1 | m0 | N |
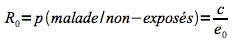
Etant donné que le calcul des risques absolus (R1 et R0) dépend de la fraction de sujets exposés ou non au facteur de risque, ils peuvent uniquement être déterminés dans le cadre d'une étude de cohorte.
Le risque relatif (RR) peut être calculé afin de mettre en évidence une association entre le facteur de risque et la maladie étudiée.
Il correspond au rapport des incidences de la maladie chez les personnes exposées (R1) et chez les personnes non-exposées (R0).
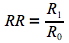
Si le risque relatif est supérieur à 1, on suppose une association entre le facteur de risque et la maladie. Toutefois, un test de Χ² est nécessaire pour vérifier si cette association est significative.
L'odds ratio correspond au rapport des cotes des risques absolus.
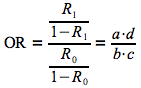
Dans le cas où la maladie étudiée est rare, le calcul de l'odds ratio permet d'estimer la valeur du risque relatif. Toutefois, quand il y a une association entre le facteur de risque et la maladie, l'odds ratio sera toujours plus élevé que le risque relatif.
Etant donné que le calcul du risque relatif dépend de la fraction de sujets exposés ou non au facteur de risque, il peut uniquement être déterminé dans le cadre d'une étude de cohorte. Lors d'une enquête cas-témoins, le risque relatif est estimé par le calcul de l'odds ratio.
Un test de Χ² est réalisé afin de vérifier si le risque relatif est significatif, autrement dit, si la probabilité d'être malade pour une personne exposée est significativement plus grande de celle d'être malade pour une personne non-exposée. Il s'agit d'un test d'indépendance comportant deux états pour chaque critère.
Hypothèse initiale (H0): RR=1. Cela signifie que la probabilité d'être malade pour une personne exposée n'est pas plus grande que la probabilité d'être malade pour une personne non-exposée; autrement dit, le fait d'être malade ne dépend pas de l'exposition ou non au facteur de risque.
Hypothèse alternative (H1): RR>1. Cela signifie que la probabilité d'être malade pour une personne exposée est supérieure à la probabilité d'être malade pour une personne non-exposée; autrement dit, il y a dépendance entre l'apparition de la maladie et l'exposition au facteur de risque.
La détermination du Χ² observé peut se faire selon la procédure détaillée au module 135 ou en utilisant la formule suivante.
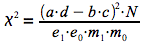
Le Χ² calculé peut alors être comparé à une valeur seuil (table de Χ²) pour 1 dl et une confiance de 95%, 99% ou 99,9%.
Le risque relatif étant une estimation, il est nécessaire de déterminer son intervalle de confiance.
Cette méthode peut être appliquée aussi bien lors d'une étude de cohorte que lors d'une enquête cas-témoins.
Les limites inférieure (RRi) et supérieure (RRs) de l'intervalle de confiance sont déterminées au moyen de la formule suivante.
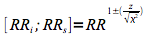
Cette méthode ne peut être appliquée que dans le cadre d'une étude de cohorte.
Les limites inférieure (RRi) et supérieure (RRs) de l'intervalle de confiance sont déterminées au moyen de la formule suivante.
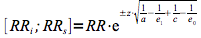
Cette méthode ne peut être appliquée que dans le cadre d'une enquête cas-témoins.
Les limites inférieure (RRi) et supérieure (RRs) de l'intervalle de confiance sont déterminées au moyen de la formule suivante.
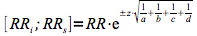
Le risque attribuable (RA), aussi appelé fraction étiologique, correspond à la proportion des cas qui seraient évités si le facteur de risque était absent.
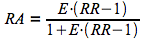
On note E, la proportion de sujets exposés dans la population. Si la maladie est rare, celle-ci peut être estimée par la proportion de personnes exposées parmi les personnes non-malades.
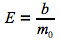
Le risque attribuable peut également être calculé à partir de la formule suivante.
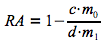
Le risque attribuable ne peut pas être déterminé dans le cadre d’une étude de cohorte. En effet, dans une telle étude, la proportion de sujets exposés dans la population n’est pas connue. L’exposition est un facteur arbitraire; c'est l'expérimentateur qui décide du nombre de personnes exposées dans son étude.
| Etude de cohorte | Enquête cas-témoins | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Table de contingence |
|
|
||||||||||||||||||||||||
| Risques absolus | 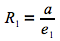 |
Ne peuvent être déterminés | ||||||||||||||||||||||||
| Risque relatif | 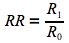 |
Si la maladie est rare: 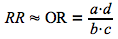 |
||||||||||||||||||||||||
| Χ2 | 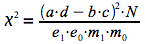 |
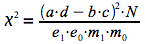 |
||||||||||||||||||||||||
| Limites intervalle de confiance | 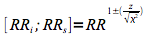 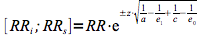 |
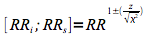 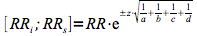 |
||||||||||||||||||||||||
| Risque attribuable | Ne peut être déterminé | 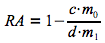 |
Afin d'étudier les risques de l'accouchement liés à l'age de la mère, une équipe de chercheurs a suivi 180 femmes camerounaises de plus de quarante ans et 532 agées entre vingt et trente ans. Parmi les femmes de plus de quarante ans, 29 ont dû accoucher par césarienne. Parmi les femmes plus jeunes, 53 ont eu recours à cette technique.
Afin d'étudier les risques de l'accouchement liés à l'age de la mère, une équipe de chercheurs a suivi 180 femmes camerounaises de plus de quarante ans et 532 agées entre vingt et trente ans. 52 femmes ont donné naissance à un fœtus sans vie (=mortinatalité) dont 21 mères de plus de quarante ans.
Afin de mettre en évidence un lien entre une exposition à des vapeurs de diesel et l'apparition d'un cancer des poumons, une équipe de chercheurs suédois a mené une étude sur 1042 personnes atteintes d'un cancer des poumons et 2364 personnes saines. Ils ont dénombré respectivement 200 et 373 personnes ayant été exposées à des vapeurs de diesel.
Afin d'étudier les risques de l'accouchement liés à l'age de la mère, une équipe de chercheurs a suivi 180 femmes camerounaises de plus de quarante ans et 532 agées entre vingt et trente ans. Parmi les femmes de plus de quarante ans, 29 ont dû accoucher par césarienne. Parmi les femmes plus jeunes, 53 ont eu recours à cette technique.
Deux groupes de femmes sont analysés: un groupe de femmes exposées (plus de quarante ans) et un groupe de femmes non-exposées (agées entre vingt et trente ans). Il s'agit donc d'une étude de cohorte.
| Césarienne | Pas de césarienne | ||
|---|---|---|---|
| Exposée (>40 ans) | 29 | 151 | 180 |
| Non-exposée (20-30 ans) | 53 | 479 | 532 |
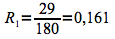
La probabilité de recours à une césarienne pour une femme de plus de quarante ans est donc de 16,1%.
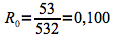
La probabilité de recours à une césarienne pour une femme agée entre vingt et trente ans est donc de 10,0%.
Le risque relatif (RR) est le rapport des incidences de la maladie étudiée (dans ce cas, le recours à une césarienne) pour les personnes exposées ou non au facteur de risque (dans ce cas, l'age de la mère). Il s'agit donc du rapport des risques absolus.
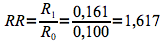
Le risque relatif étant plus grand que 1, on peut supposer une association entre l'age élevé de la mère et le recours à une césarienne.
Pour savoir si ce risque relatif est significatif ou non, on réalise un test de Χ².
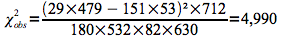
Comme la valeur du Χ² observé est plus grande que la valeur de Χ² seuil (Χ²(1;0,95)=3,84), on peut conclure que le risque de recours à une césarienne est significativement plus élevé chez les femmes de plus de quarante ans que chez les femmes agées entre vingt et trente ans.
Détermination des limites de l'intervalle de confiance du risque relatif par la méthode de Miettinen.
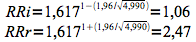
L'intervalle de confiance du risque relatif est compris entre 1,06 et 2,47 (méthode de Miettinen).
Détermination des limites de l'intervalle de confiance du risque relatif par la méthode de Katz.
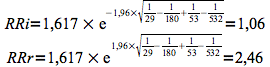
L'intervalle de confiance du risque relatif est compris entre 1,06 et 2,46 (méthode de Katz).
Dans le cadre d'une étude de cohorte, la fraction de sujets exposés dans la population (E) n'est pas connue. Le risque attribuable, qui dépend de cette fraction, ne peut donc pas être déterminé.
Afin d'étudier les risques de l'accouchement liés à l'age de la mère, une équipe de chercheurs a suivi 180 femmes camerounaises de plus de quarante ans et 532 agées entre vingt et trente ans. 52 femmes ont donné naissance à un fœtus sans vie (=mortinatalité) dont 21 mères de plus de quarante ans.
Deux groupes de femmes sont analysés: un groupe de femmes exposées (plus de quarante ans) et un groupe de femmes non-exposées (agées entre vingt et trente ans). Il s'agit donc d'une étude de cohorte.
| Foetus sans vie | Foetus en vie | ||
|---|---|---|---|
| Exposée (>40 ans) | 21 | 159 | 180 |
| Non-exposée (20-30 ans) | 31 | 501 | 532 |
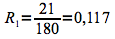
La probabilité de mettre au monde un fœtus sans vie pour une femme de plus de quarante ans est donc de 11,7%.
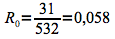
La probabilité de mettre au monde un fœtus sans vie pour une femme agées entre vingt et trente ans est donc de 5,8%.
Détermination du risque relatif:
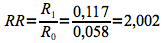
Le risque relatif étant plus grand que 1, on peut supposer une association entre l'age élevé de la mère et la naissance d'un fœtus sans vie.
Calcul de la valeur de Χ² observée:
![]()
Comme la valeur du Χ² observé est plus grande que la valeur de Χ² seuil (Χ²(1;0,95)=3,84), on peut conclure que le risque de mortinatalité est significativement plus élevé chez les femmes de plus de quarante ans que chez les femmes agées entre vingt et trente ans.
Détermination des limites de l'intervalle de confiance du risque relatif par la méthode de Miettinen:
![]()
L'intervalle de confiance du risque relatif est compris entre 1,19 et 3,38 (méthode de Miettinen).
Détermination des limites de l'intervalle de confiance du risque relatif par la méthode de Katz:
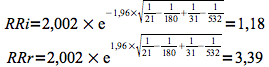
L'intervalle de confiance du risque relatif est compris entre 1,18 et 3,39 (méthode de Katz).
Dans le cadre d'une étude de cohorte, la fraction de sujets exposés dans la population (E) n'est pas connue. Le risque attribuable, qui dépend de cette fraction, ne peut donc pas être déterminé.
Afin de mettre en évidence un lien entre une exposition à des vapeurs de diesel et l'apparition d'un cancer des poumons, une équipe de chercheurs suédois a mené une étude sur 1042 personnes atteintes d'un cancer des poumons et 2364 personnes saines. Ils ont dénombrés respectivement 200 et 373 personnes ayant été exposées à des vapeurs de diesel.
Un groupe de personnes malades (cas) et un groupe de personnes non-malades (témoins) sont constitués et on recherche si elles ont été exposées à des vapeurs de diesel par le passé. Il s'agit donc d'une enquête cas-témoins.
| Malade (cancer des poumons) | Non-malade (pas de cancer des poumons) | |
|---|---|---|
| Exposé (aux vapeurs de diesel) | 200 | 373 |
| Non-exposé (aux vapeurs de diesel) | 842 | 1991 |
| 1042 | 2364 |
Les risques absolus (R1 et R0) ne peuvent être déterminés dans le cadre d'une étude cas-témoins.
Le risque relatif, dépendant de R1 et R0, ne peut être calculé. Toutefois, dans le cas où la maladie est rare, il peut être estimé par le calcul de l'odds ratio.
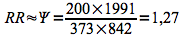
Grâce au calcul de l'odds ratio, le risque relatif peut être estimé à 1,27. Le risque relatif estimé étant plus grand que 1, on peut supposer une association entre l'exposition à des vapeurs de diesel et l'apparition d'un cancer des poumons.
Calcul de la valeur de Χ² observé:
![]()
Comme la valeur du Χ² observé est plus grand que la valeur de Χ² seuil (Χ²(1;0,95)=3,84), on peut conclure que le risque d'apparition d'un cancer des poumons est significativement plus élevé chez les personnes exposées aux vapeurs de diesel que chez les personnes non-exposées à ces vapeurs.
Détermination des limites de l'intervalle de confiance du risque relatif par la méthode de Miettinen:
![]()
L'intervalle de confiance du risque relatif est compris entre 1,049 et 1,532 (méthode de Miettinen).
Détermination des limites de l'intervalle de confiance du risque relatif par la méthode de Woolf:
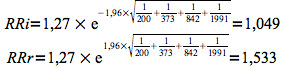
L'intervalle de confiance du risque relatif est compris entre 1,049 et 1,533 (méthode de Woolf).
Cette proportion correspond au risque attribuable (RA).
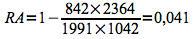
Cela signifie que 4,1% des cas de cancer des poumons sont imputables à l'exposition aux vapeurs de diesel.