Un écologiste étudie une population de chauves-souris de l'espèce Grand Rhinolophe. D'après la littérature, il sait que l'envergure de ces chiroptères obéit à une distribution normale dont la moyenne est de 375 mm pour une variance de 225 mm2.

Cet écologiste capture un individu dont la taille est de 350 mm. Cet individu est-il considéré comme conforme ou bien est-il significativement différent de ce que prévoit le modèle?

Les hypothèses:

H0: µ1 = µ (l'individu a une taille conforme)

H1: µ1 différent de µ (l'individu est non conforme)

Attention: "significativement" qualifie une confiance de 95%, par conséquent le alpha = 5%

Ou encore

Ho : M1 = M    H1 : M1 > M    H2 : M1 < M

Convertir la valeur observée en une valeur réduite:

X observé = 350 mm

z observé = (350-375)/15 (où 15 est l'écart-type de la population)

 

z observé = -1,66666667

Trouver le seuil de signification:

On sait que alpha vaut 5%. Le test est bidirectionnel (H1 ou H2). Le seuil de signification est donc z alpha/2 pour H2 et z (1-alpha/2) pour H1

Dans la table, on ne peut trouver que les probabilités P(Z<z) pour z positif. La borne supérieure de l'intervalle de confiance vaut 1,96. En utilisant la propriété de symétrie la borne inférieure vaut -1,96.

Conclusion:

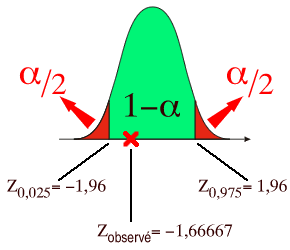-1,96<-1,66666667<1,96 c'est-à-dire z observé compris entre les bornes de l'intervalle de confiance On accepte H0 (AH0) Cela veut dire qu'on n'a pas réussi à montrer que l'individu capturé était significativement (alpha de 5%) différent de la normale.