Dans le cadre complexe des régressions, nous n'aborderons ici que le cas particulier de la régression linéaire, dont les principes de base ont été définis dans le module 20 : Statistiques descriptives à deux dimensions. On abordera plus particulièrement le cas d'une régression à X fixé, tel que décrit dans le module 170 : Régression dans l'ANOVA 1.
Régression linéaire à X fixé :
Dans ce cas particulier les conditions d'inférence sur la droite de régression sont strictes :
Condition 1 :
Les valeurs prises par la variable X doivent être fixées sans erreur par l'expérimentateur.
Condition 2 :
X étant une variable contrôlée (valeurs fixées par l'expérimentateur), on peut considérer Y comme fonction de X, mais pas le contraire : Y=f(X)
Condition 3:
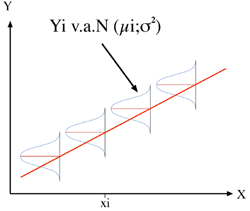
Pour chaque valeur Xi de X, il existe une population de valeurs Yi distribuée normalement, de moyenne µi et de variance σ2 homogène c'est-à-dire constante quelle que soit la valeur de X :
Yi v.a.N(µi ;σ2 )
Condition 4:
Les moyennes µi correspondant aux valeurs Yi sont situées sur une droite dont les paramètres sont ß0 et ß1 telle que :
µi =ß0+ß1.Xi
avec ß0 l'ordonnée à l'origine et ß1 la pente.
Dans ces conditions, la pente ß1 = B1 ± ε avec 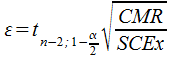
avec : 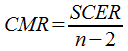
et : 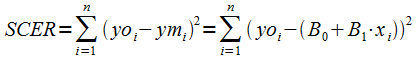
avec :
- yo = y observé
- ym = y estimé par l'équation de la régression pour le même x que le yo
- ye = yo-ym
Exemple
Un démographe estime la croissance de la population pensionnée d'un quartier, année par année sur 5 ans :
Yo = 26%, 32%, 40%, 44%, 55% :
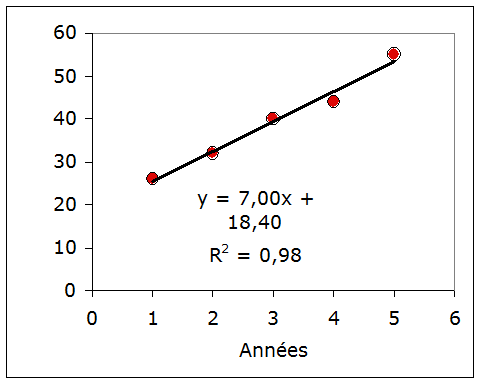
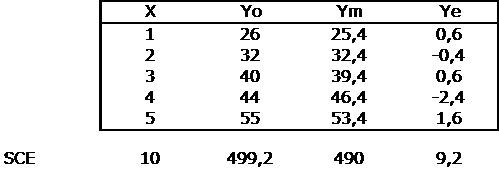
Sur base du modèle linéaire Ym = Bo + B1.X, il estime une croissance de 7,00 % par an (B1).
Tables : t3 ;0,975 = 3,18
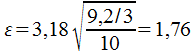
L'accroissement réel annuel est donc compris entre 5,24 et 8,76%

