Principe général :
Le principe de l'intervalle de confiance d'un paramètre d'une population est toujours le même. La formulation générale en est :
La valeur vraie du paramètre = statistique de l'échantillon ± une imprécision (ε).
La probabilité que cette affirmation soit vraie est la confiance. L'imprécision ε est d'autant plus grande que la confiance souhaitée est élevée.
Cas particulier d'un dénombrement :
L'intervalle de confiance d'un dénombrement µ est : µ = x ± ε
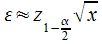
Exemple :
Un géologue mesure une radioactivité de 150 dpm dans un prélèvement de roche. Que peut-il dire de la valeur réelle de la radioactivité ?
Exactement : la valeur de z = 1,96
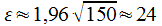
Approximativement : la valeur de Z est arrondie à 2.
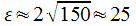
La radioactivité réelle a 95 chances sur 100 d'être comprise entre 125 et 175 dpm.
|

