Lorsque la variance de la population (σ2) est inconnue, elle est estimée par celle de l'échantillon (S2), et l'erreur type est alors estimée par :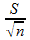 
Ceci signifie que d'un échantillon à l'autre, la longueur de l'intervalle de confiance sera variable, car elle dépendra de n (nombre d'individus dans l'échantillon) et de S (écart-type de l'échantillon), qui varient d'un échantillon à l'autre.
Pour tenir compte de cette variabilité de la variance estimée, la longueur de l'intervalle de confiance est calculée sur la distribution de la variable t de Student.
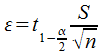avec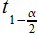 
la valeur de t en dessous de laquelle il y a 1-α/2 % des individus.
Si le nombre d'observations disponibles pour estimer la variance est faible, la longueur de l'intervalle de confiance à 95% est donc plus élevée que 2 erreurs types.
Par exemple, pour n = 3, la limite supérieure est un t2; 0,975 = 4,303.
Cette longueur accrue de l'intervalle de confiance fait qu'il y aura toujours 95% de chance d'inclure la vraie moyenne µ.
Le prix à payer pour conserver cette confiance de 95% est une plus grande imprécision de l'estimation de μ.
Pour obtenir une confiance de 99%, il faudra accepter une plus grande imprécision.
Par exemple, pour n = 3, la limite supérieure est un t2; 0,995 = 9,925.
Exemple
Le dosage de protéines de 4 échantillons récoltés au hasard dans le stock de lait d'une laiterie donne les statistiques suivantes :
Mx=30 g/l et S2= 16 (g/l)2
La variable mesurée est supposée normale : X v.a. N ( μ,σ2 ).
Que peut-on dire de la moyenne réelle de la teneur en protéines du stock de la laiterie ?
A priori, l'expérimentateur doit savoir que le paramètre µ ne vaut pas exactement 30g/l. Il peut cependant affirmer que :
µ = 30 ± une certaine imprécision ( ε )
Dans notre exemple S = 4 g/l, n = 4 et la variable t a 3 degrés de liberté (d.l.). La borne supérieure de l'intervalle à 95% se trouve dans les tables :
t3; 0,975 = 3,18
L'erreur type estimée = S/√n = 4/2 g/l et ε = 3.18 x 2 = 6,36 g/l.
La moyenne réelle de la teneur en protéines du stock de la laiterie est donc comprise entre les limites
30 g/l ± 6,36 g/l soit entre 23,64 g/l et 36,36 g/l.
La confiance dans cette estimation est de 95%. Autrement dit, il y a 5% de risque que la teneur en protéines soit moins de 23,64 g/ ou plus de 36,36 g/l .
