Pour illustrer les mesures de dispersion, prenons pour exemple un échantillon de 9 morues de l'Atlantique (Gadus morhua).

Pour cet échantillon de 9 morues, nous allons étudier la dispersion de la taille de ces poissons en calculant les paramètres suivants :
Nous verrons ensuite un paramètre de dispersion additionnel, le coefficient de variation, utilisé dans le cas particulier des échantillons de mesures répétées.
Pour commencer, mesurons la taille de ces 9 poissons, ainsi que la moyenne de ces tailles, qui vaut ici 65 cm :
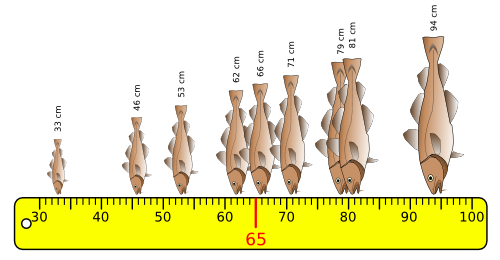
L'amplitude :
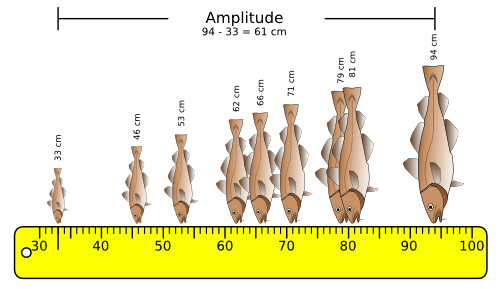
Définition : L'amplitude d'un échantillon est l'écart qui sépare la valeur la plus petite de la valeur la plus grande.
Formule : amplitude = valeur maximale - valeur minimale
Domaine : L'amplitude peut prendre des valeurs qui vont de 0 à l'infini.
La variance :
Définition : La variance est le reflet numérique de la dispersion des valeurs autour de la moyenne.
Elle est obtenue à partir des écarts des valeurs par rapport à la moyenne.
Ecarts à la moyenne :
Pour chaque valeur on calcule l'écart qui le sépare de sa moyenne arithmétique : ei = xi - Mx
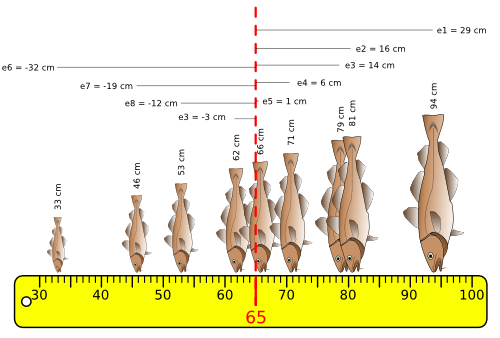
La somme de ces écarts est nulle. Elle ne peut donc être utilisée comme un estimateur mathématique de la dispersion des valeurs.
Carrés des Ecarts à la moyenne :
Pour chacun des écarts on calcule son carré. Ainsi pour chaque valeur on obtient une valeur positive, et leur somme n'est jamais nulle, sauf si les écarts sont nuls (valeurs identiques).
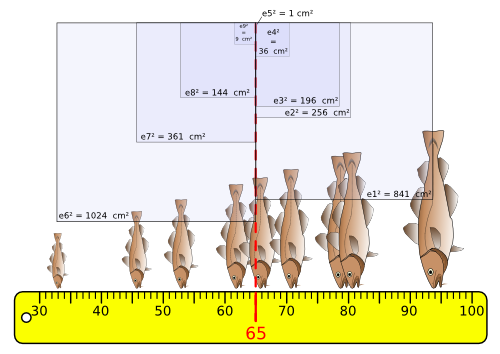
Si on additionne tous ces carrés d'écarts :
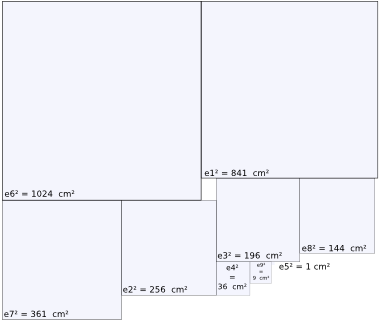
Cela donne :

La somme des carrés des écarts (SCE) sera d'autant plus grande que les valeurs seront éloignées de la moyenne. C'est donc un bon estimateur de la dispersion des valeurs autour de la moyenne.
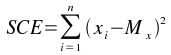
Cependant, à dispersion équivalente, la SCE sera toujours d'autant plus grande qu'il y aura un nombre important de valeurs. Pour que le paramètre de dispersion soit indépendant du nombre de valeurs, on calcule le carré moyen.
Carré moyen :
Le carré moyen représente la surface moyenne des carrés d'écarts. C'est la SCE/n.
La variance d'un échantillon (ou S 2) est la surface de ce carré moyen (CM).
Elle caractérise la distribution des valeurs autour de la moyenne.
Elle est exprimée dans le carré des unités des valeurs, ici en cm2.
Formule : Elle se calcule en sommant les carrés des écarts (SCE = Somme de Carrés des Écarts), et en divisant cette somme par le nombre de valeurs.
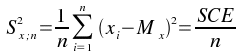
Domaine : La variance est comprise entre 0 et l'infini.
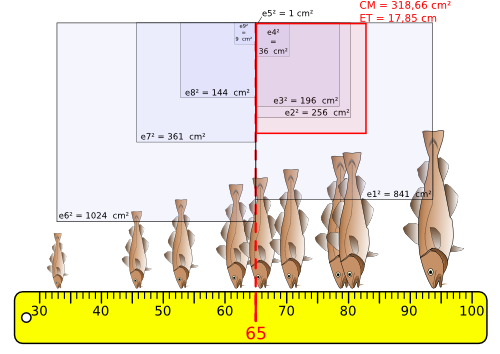
A partir des données numériques d'un échantillon, il est aussi possible d'estimer la variance de la population d'où provient cet échantillon.
On utilise alors une autre formule :
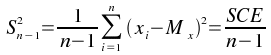
L'écart-type :
La variance étant exprimée dans le carré des unités, on lui préfère souvent l'écart-type, qui s'exprime lui dans l'unité des valeurs
Définition : L'écart-type représente l'écart moyen des valeurs par rapport à la moyenne. Il est exprimé dans les unités de la moyenne.
Formule : L'écart-type (ET ou S) est la longueur du côté du carré moyen, et donc la racine carrée de la variance.
Pour décrire un échantillon :
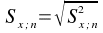
Pour estimer l'écart-type de la population d'origine :
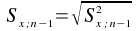
Domaine : L'écart-type est compris entre 0 et l'infini.
Le coefficient de variation :
Définition : Le coefficient de variation représente le rapport de l'écart-type par la moyenne.
Formule :
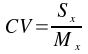
Domaine : Le coefficient de variation est compris entre 0 et l'infini.
Utilisation : Le CV est utilisé pour quantifier la précision d'appareils de mesure. Lorsqu'on mesure plusieurs fois un même objet de taille connue, si le CV tend vers 0 c'est que l'appareil est précis. S'il tend vers 1 ou vers l'infini c'est que l'appareil est imprécis.

