La classification des données x_i (poids des morues pêchées) est obtenue en créant artificiellement des classes (ou catégories) d'individus.

Le nombre de classes dépend du nombre d'individus pêchés:

• il ne peut être trop petit sous peine de perdre de l'information: 1 classe contenant tous les individus de l'échantillon revient à ne pas faire de classes.
• il ne peut être trop grand sous peine de perdre de l'information: pour un échantillon de 15 individus, réaliser 15 classes revient à avoir des classes ne contenant même pas un poisson.

 

Les classes possèdent toutes le même intervalle séparant leur limite inférieure et supérieure (dans l'exemple: l'intervalle de classe L_i vaut 2 Kg):

• classe 1: de 0 Kg inclus à 2 Kg exclus
• classe 2: de 2 Kg inclus à 4 Kg exclus
• classe 3: de 4 Kg inclus à 6 Kg exclus
• classe 4: de 6 Kg inclus à 8 Kg exclus

Le dénombrement des poissons par classe peut suivre différentes définitions:

1. fréquence: nombre d'individus appartenant à une classe. Il est généralement noté n_i . La somme des fréquences de toutes les classes est la taille de l'échantillon N.
2. fréquence cumulée: somme des fréquences de la classe étudiée et des fréquences des classes qui lui sont inférieures. La fréquence cumulée de la dernière classe vaut N (c'est-à-dire la somme des n_i).
3. la fréquence relative: rapport entre la taille de la classe étudiée et la taille de l'échantillon. Nous étudions dans ce cas l'importance de la classe par rapport à la globalité de l'échantillon (exemple: 20% des individus de l'échantillon présenté dans la figure ci-dessus ont une envergure comprise entre 380 et 400 mm). La somme de toutes les fréquences relatives est égale à 1. Elle est notée n_i/N.
4. la fréquence relative cumulée: somme des fréquences relatives de la classe étudiée et des fréquences relatives des classes qui lui sont inférieures. La fréquence relative cumulée de la dernière classe vaut 1.
5. la densité de fréquences relatives : souvent employée pour que la surface de chaque rectangle de l'histogramme corresponde à la fréquence relative de la classe:

Surface d'un rectangle = Hauteur. Base c'est-à-dire 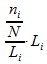ou encore (après simplification des Li) la fréquence relative ni/N.

 

Un cas extrême est celui où la taille de l'échantillon tend vers l'infini. A ce moment, le nombre de classes possibles tend aussi vers l'infini. Chaque classe possède un intervalle (une base) infinitésimal. La surface d'un rectangle tend vers 0. On ne parlera plus de distribution de densités de fréquences relatives mais de distribution de densités de probabilités.

 

L'intervalle de classe (L_i) est la distance séparant la limite supérieure de la limite inférieure de chaque classe.