Module 60:

La distribution de Poisson s'applique aux variables quantitatives discrètes définies par le nombre d'événements observés dans le cas où ces événements se produisent de manière indépendante et aléatoire dans le temps ou dans l'espace. Cette distribution est caractérisée par le seul paramètre µ qui est la moyenne de la distribution et la variance. La distribution de Poisson peut s'appliquer dans des problèmes de gestion (file d'attente, centrales téléphoniques : événement aléatoire dans le temps), en microbiologie (nombre de bactéries dans une boite de Pétri), en écologie (nombre de moules par mètres carrés), en biologie clinique (nombre de globules blancs par ml). Il s'agit donc de l'occurrence d'un événement élémentaire par unité de volume, de surface ou de temps.

Contrairement à la Binomiale, il n'y a pas ici de notion d'échec ou de succès et il n'y a pas de contrainte supérieure (le comptage est illimité).

Nomenclature :

Soit X une variable de Poisson où X = comptage dans l'intervalle considéré. Elle se caractérise par µ, qui est à la fois la moyenne et la variance de la distribution.

Notons que la variable aléatoire de Poisson a une distribution asymétrique si µ n'est pas très élevé.

X v.a. Po (µ)

• E(x) = µ et var(x) = µ
• moyenne = variance

Exemples de variables aléatoires de Poisson

Nombre d'évènements par unité (volume, temps, surface)

• Le nombre de poissons par mètre cube d'eau
• Le nombre de drosophiles mâles rencontrés pendant 10 minutes
• Le nombre de désintégrations d'un radio-isotope par minute

à ne pas confondre avec la binomiale. Exemple : le nombre de truites par 100 poissons pêchés dans une rivière

Détermination de la probabilité P(X = x)

La variable aléatoire de Poisson a comme fonction de densité de probabilité :

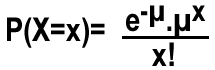
Condition: x0

le seul paramètre est µ = le nombre moyen d'événements.

Un zoologiste étudie les passages d'une espèce de chauve-souris en lisière d'un espace boisé à La Plante près de Namur. Il effectue un comptage d'individus et répertorie en moyenne 3 individus par 30 minutes (arrondir à deux décimales significatives).

1. Quelle est la probabilité qu'il détecte 7 individus en 1H?

X est une v.a. Po(6) car, en moyenne on a 3 individus détectés par demi-heure, donc 6 individus sont détectés par heure.

P(X=7)= (table) = P(X7) - P(X6)= 0,14

2. Quelle est la probabilité qu'il détecte au plus 7 individus en 1H?

P(X 7)=0,74

3. Quelle est la probabilité qu'il détecte entre 2 et 4 individus par 15 minutes?

X est une v.a. Po(1,5) car, en moyenne on a 3 individus détectés par demi-heure, donc 1,5 individus sont détectés par tranches de 15 minutes.

P(2X4)=P(X4)-P(X1)=0,98 - 0.56 = 0.42

1. L'institut National de Statistiques s'est intéressé au nombre d’accidents sur la route et démontre qu'en moyenne, on observe 2 accidents par quart d'heure en pleine heure de pointe.

- Quelle est la probabilité de n'observer aucun accident en un quart d'heure?
solution: P(X=0) = 0,135

- Quelle est la probabilité d'observer plus de 3 accidents en un quart d'heure?
solution: P(X>3) = 0,143

- Quelle est la probabilité de n'observer aucun accident en une heure?
solution: P(X = 0) = 0,0003

- Quelle est la probabilité d'observer 4 accidents en une heure?
solution: P(X = 4) = 0,0572


2. Selon les observations, en moyenne 3 personnes entrent dans la gare de Namur toutes les 5 minutes. Sachant cela,

- Quelle est la probabilité qu'aucun individu n'entre dans la gare durant les 5 minutes d'observation?
solution: P(X=0) = 0,0498

- Quelle est la probabilité que 4 personnes et plus entrent dans la gare de Namur durant ces 5 minutes?
solution: P(X >= 4) = 0,35


3. Soit X le nombre de mollusques capturés par 10 dm2.
Supposons que la répartition des animaux est non agrégative et que la concentration moyenne est de 10 individus par 10 dm2. Quelle est la probabilité de capturer 15 individus par 10 dm2?
solution: P(X=15) = 0,035