imprimer

Module 150:

Cette méthode de comparaison des moyennes est peu sensible à la non normalité et à l'inégalité des variances comparées. Elle est applicable même dans le cas où les effectifs des échantillons ne sont pas tous égaux (Scheffé 1953).

Définition

Il s'agit d'un test de comparaison de moyennes 2 à 2. Soit les deux moyennes testées sont identiques (H0) soit elles sont différentes (H1).

Principe

Ce test permet de comparer la différence entre 2 moyennes par rapport à une valeur seuil appelée PPDS: Plus Petite Différence Significative
moyenne 1
moyenne 2
moyenne 3
moyenne 1
0
moyenne 2
moy1-moy2
0
moyenne 3
moy1-moy3
moy2-moy3
0

Chaque différence entre deux moyennes est comparée à la PPDS.

Si la différence est plus grande que la PPDS, on considère que l'écart séparant les deux échantillons est significatif ou hautement significatif suivant le alpha utilisé pour déterminer la valeur de la PPDS.

L'utilisation des contrastes de SCHEFFE sur MS Excel se réalise comme suit:

Aligner les moyennes de l'expérience
moyenne 1
moyenne 2
moyenne 3
moyenne 1
moyenne 2
moyenne 3

 

Réaliser les différences entre les moyennes 2 à 2
moyenne 1
moyenne 2
moyenne 3
moyenne 1
m1-m1
m2-m1
m3-m1
moyenne 2
m1-m2
m2-m2
m3-m2
moyenne 3
m1-m3
m2-m3
m3-m3

Ampoule pour éviter d'avoir à traiter des valeurs négatives vous pouvez employer la fonction Excel =ABS(votre calcul) qui transforme le résultat de votre calcul en une valeur absolue.
moyenne 1
moyenne 2
moyenne 3
moyenne 1
ABS(m1-m1)
ABS(m2-m1)
ABS(m3-m1)
moyenne 2
ABS(m1-m2)
ABS(m2-m2)
ABS(m3-m2)
moyenne 3
ABS(m1-m3)
ABS(m2-m3)
ABS(m3-m3)

 

Calculer la PPDS (Plus Petite Différence Significative)

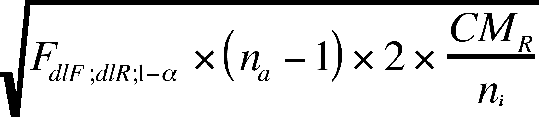
Formule pour calculer la PPDS

Ce qui équivaut à faire dans Excel:

= RACINE(INVERSE.LOI.F(alpha,dlF,dlR)*(na-1)*2*(CMR/ni))

où vous devez remplacer alpha, dlF, dlR, na, CMR et ni par leur valeur respective.

ATTENTION: selon les versions et les réglages d'Excel le séparateur de alpha et des dl est parfois une virgule, parfois un point-virgule.

A la place de la formule INVERSE.LOI.F(alpha,dlF,dlR) vous pouvez aussi déterminer dans les tables la valeur de F à utiliser.

Calculez les PPDS qui correspondent à un alpha de 5% et de 1% (NDLR: valeur à rentrer dans Excel: 0,05 et 0,01).

Conclusion du test de SCHEFFE:

Lorsqu'une des différences est plus grande que la PPDS, cela signifie que les 2 moyennes comparées sont différentes de façon significative, ou hautement significative, selon que la PPDS utilisée est celle calculée pour alpha=5% ou celle calculée pour alpha=1%.

Exemple de conclusion du test de SCHEFFE:
moyenne 1
moyenne 2
moyenne 3
moyenne 1
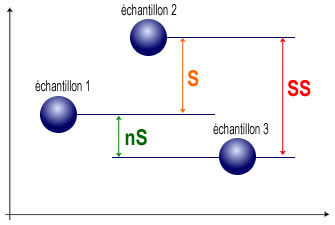
 0    
moyenne 2
 S 0  
moyenne 3
 nS SS 0

 

Les contrastes de SCHEFFE mettent en évidence une différence significative entre les échantillons 1 et 2 ainsi qu'une différence très significative entre les échantillons 2 et 3. Les échantillons 1 et 3 possèdent des moyennes comparables.

distances entre échantillons non significative, significative ou hautement significative

 

Pourquoi regrouper?

Le groupement lors de l'analyse des contrastes de Scheffé permet d'augmenter la puissance du test et de se poser a posteriori des questions plus élaborées.

Méthodologie:

Lors d'une étude sur l'effet de la teneur en calcium dans la nourriture des brebis, le poids frais (g) du muscle semi-tendineux est quantifié sur 6 groupes de 7 animaux, chaque groupe recevant du calcium à une dose et un type d'administration qui lui sont spécifiques.

 
Témoin
Additif
Comprimé
Liquide
dose 1
dose 2
dose 1
dose 2
moyenne
140,0
143,4
145,1
139,3
147,6
147,9
variance
3,0
7,0
3,2
5,7
5,6
3,8

 

Le test de Hartley est non significatif: la condition d'homoscédasticité est donc remplie.

L'ANOVA 1 est significative: au moins une des moyennes de poids diffère.
Il est donc intéressant d'étudier les contrastes de Scheffé de manière groupée.

Scheffé groupé

H0: les deux groupes comparés sont de moyenne égale
H1: les deux groupes comparés ont des moyennes différentes

 
Témoin
140,0
Additif
Comprimé
139,3
Liquide
L
Σci2
PPDS
groupé
Ccl
 
dose 1
143,4
dose 2
145,1
dose 1
147,6
dose 2
147,9
Q1
5
-1
-1
-1
-1
-1
-23,3
30
15,7
*
Q2
0
2
2
2
-3
-3
-30,9
30
15,7
*
Q3
0
-1
-1
2
0
0
-9,9
6
7,0
*
Les questions:

Q1: Y a-t-il un effet significatif de l'administration de calcium sur le poids des muscles?
Q2: L'administration du calcium sous forme liquide a-t-elle un effet différent de l'administration de Ca sous une autre forme?
Q3: L'administration du Ca sous forme de comprimé a-t-elle un effet différent sur le poids des muscles par rapport à l'administration sous forme d'additif?

Les calculs:

L

Σ(moyenne observée * ci )

PPDS groupé

racine( (na-1) * CMR * Σci2 * F( na-1; N-na;1-α) /  ni)

 

Les conclusions:

Q1: nous observons un effet significatif de l'administration de calcium sur les poids des muscles et ce, quelle que soit la méthode d'administration
Q2: nous constatons que les effets de l'apport en calcium sont significativement plus élevés lorsqu'il est fourni sous forme liquide par rapport aux additifs et aux comprimés
Q3: nous constatons que l'effet sur le poids des muscles est significativement plus important lorsque l'apport se fait sous forme d'additifs par rapport aux apports sous forme de comprimés

Formules utiles dans Excel coller une fonction:

Afin d'alléger les calculs dans Excel, utilisez de préférence les formules "prêtes à l'emploi" disponibles via le bouton "coller une fonction" (fx).

ABS(...) permet de faire calculer la valeur absolue

SOMMEPROD(matrice1; matrice2) permet de calculer une somme de produits de valeurs provenant de 2 matrices de données distinctes (exemple: matrice1= valeur1; valeur2 et matrice2= valeur3; valeur4. Suivant la formule, on calcule (valeur1*valeur3+valeur2*valeur4)

SOMME.CARRES(série de données) permet de calculer la somme des carrés des valeurs sélectionnées